琉球大学
琉球大学
大学入試問題#910「いやーいかにもミスりそう」 #琉球大学2021
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#琉球大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} |3\sin x+\cos x| dx$
出典：2021年琉球大学後期
この動画を見る
$\displaystyle \int_{0}^{\pi} |3\sin x+\cos x| dx$
出典：2021年琉球大学後期
#茨城大学2022#極限_10#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to -\infty } \displaystyle \frac{4^{x+2}+2^{x-2}}{4^x-2^x}$
出典：2022年茨城大学
この動画を見る
$\displaystyle \lim_{ x \to -\infty } \displaystyle \frac{4^{x+2}+2^{x-2}}{4^x-2^x}$
出典：2022年茨城大学
【高校数学】毎日積分57日目~47都道府県制覇への道~【①沖縄】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$a$を実数とし、$f(x)=xe^{-|x|}, g(x)=ax$とおく。次の問いに答えよ。
問1 $f(x)$の増減を調べ、$y=f(x)$のグラフの概形をかけ。ただし$\displaystyle \lim_{x\to \infty}xe^{-x}=0$は証明なしに用いてよい。
問2 $0＜a＜1$のとき、曲線$y=f(x)$と直線$y=g(x)$で囲まれた2つの部分の面積の和を求めよ。
【琉球大学 2023】
この動画を見る
$a$を実数とし、$f(x)=xe^{-|x|}, g(x)=ax$とおく。次の問いに答えよ。
問1 $f(x)$の増減を調べ、$y=f(x)$のグラフの概形をかけ。ただし$\displaystyle \lim_{x\to \infty}xe^{-x}=0$は証明なしに用いてよい。
問2 $0＜a＜1$のとき、曲線$y=f(x)$と直線$y=g(x)$で囲まれた2つの部分の面積の和を求めよ。
【琉球大学 2023】
大学入試問題#377「基本的な手筋」 琉球大学(2015) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1}|x|\sqrt{ 1-x^2 }\ dx$
出典：2015年琉球大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1}|x|\sqrt{ 1-x^2 }\ dx$
出典：2015年琉球大学 入試問題
大学入試問題#227 琉球大学(2012) 方程式
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師：
ますただ
問題文全文(内容文)：
方程式
$log_5(1-4・5^x)=2x+1$を解け
出典：2012年琉球大学 入試問題
この動画を見る
方程式
$log_5(1-4・5^x)=2x+1$を解け
出典：2012年琉球大学 入試問題
大学入試問題#203 琉球大学(2020) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{log2}^{log3}\displaystyle \frac{xe^x}{(e^x-1)^2}dx$を計算せよ
出典：2020年琉球大学 入試問題
この動画を見る
$\displaystyle \int_{log2}^{log3}\displaystyle \frac{xe^x}{(e^x-1)^2}dx$を計算せよ
出典：2020年琉球大学 入試問題
琉球大 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
pは素数であり,nを自然数とする.
$f(n)=n^p-n,f(n+1)-f(n)$はpの倍数であることを示せ.
琉球大過去問
この動画を見る
pは素数であり,nを自然数とする.
$f(n)=n^p-n,f(n+1)-f(n)$はpの倍数であることを示せ.
琉球大過去問
大学入試問題#155 琉球大学(1987) 極限
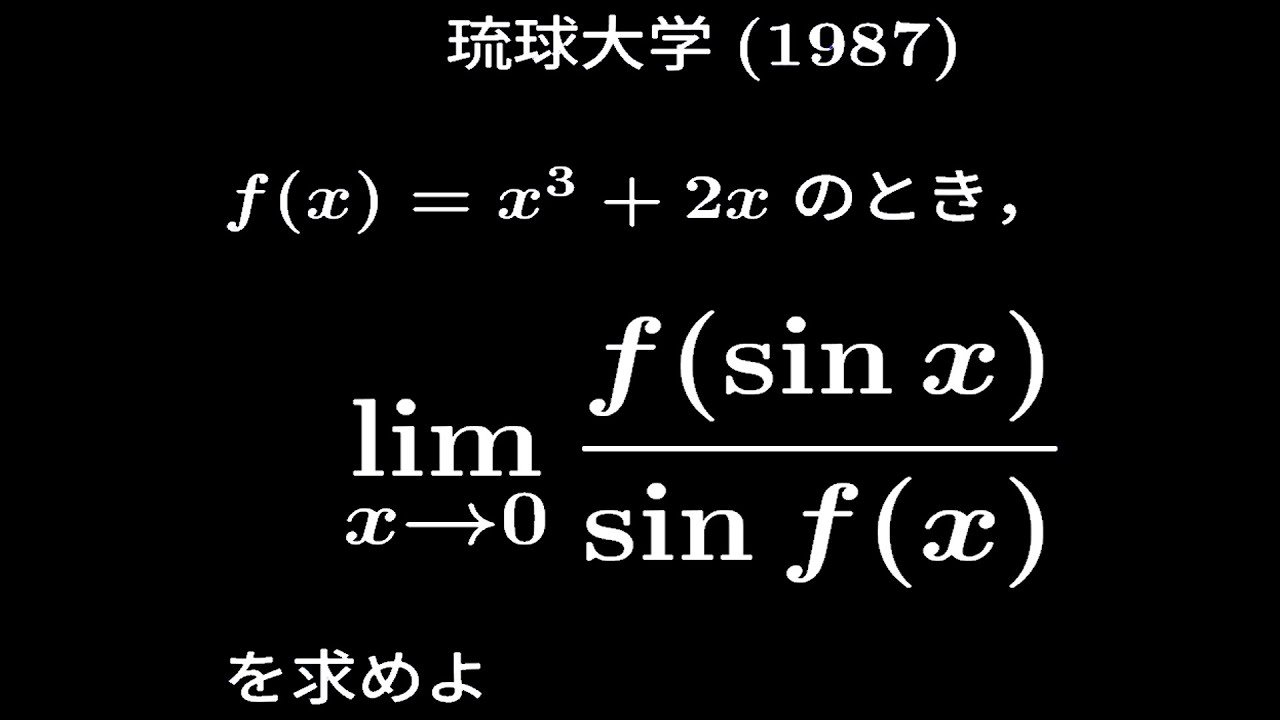
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x^3+2x$のとき
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(\sin\ x)}{\sin\ f(x)}$を求めよ。
出典：1987年琉球大学 入試問題
この動画を見る
$f(x)=x^3+2x$のとき
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(\sin\ x)}{\sin\ f(x)}$を求めよ。
出典：1987年琉球大学 入試問題
琉球大 微分・積分 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#琉球大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
琉球大学過去問題
-2<a<2
$y=x^2+ax+1$に原点から引いた2本の接線の接点をP,Qとする。
(1)2つの接点P,Qの座標を求めよ。
(2)2本の接線と放物線で囲まれた図形の面積
この動画を見る
琉球大学過去問題
-2<a<2
$y=x^2+ax+1$に原点から引いた2本の接線の接点をP,Qとする。
(1)2つの接点P,Qの座標を求めよ。
(2)2本の接線と放物線で囲まれた図形の面積