愛知教育大学

単元： #大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知教育大学

指導講師：ますただ

問題文全文(内容文)：

\int_{- 1}^{1} \frac{x^{2}}{1 + e^{x}} d x

出典：2023年愛知教育大学　入試問題

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#愛知教育大学

指導講師：ますただ

問題文全文(内容文)：

α = \sqrt[3]{5 \sqrt{2} + 7} - \sqrt[3]{5 \sqrt{2} - 7}

（1）

α^{3}

を

α

で表せ
（2）

α

は整数であることを示せ

出典：2012年愛知教育大学　入試問題

この動画を見る　

単元： #大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知教育大学

指導講師：ますただ

問題文全文(内容文)：

lim_{n \to \infty} \sum_{k = 1}^{n} \frac{1}{n + k} (l o g (n + k) - l o g n)

を求めよ。

出典：2013年愛知教育大学　入試問題

この動画を見る　

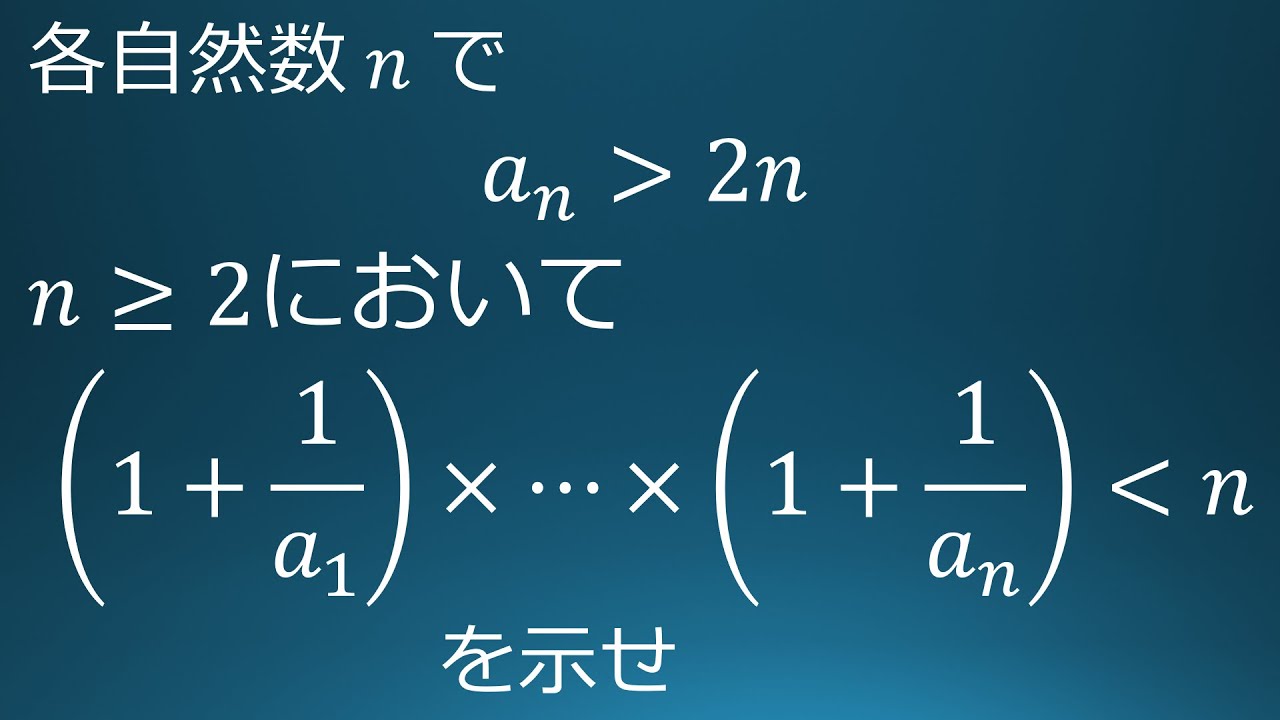
単元： #数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)#愛知教育大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
不等式を解け

a \neq 0, 1

a (a - 1) x^{2} + (2 - 3 a) x + 2 < 0

出典：2018年愛知教育大学　過去問

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#愛知教育大学

指導講師：鈴木貫太郎

問題文全文(内容文)：

x^{3} - 3 a x + 4 \sqrt{2} = 0

実数解の個数

出典：2002年愛知教育大学　過去問

この動画を見る　