 長崎県公立高校
長崎県公立高校
 長崎県公立高校
長崎県公立高校
【その場でシコウするには…!】整数:長崎県~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
各位の数の和が5である4けたの自然数のうち,
大きい方から数えて5番目の自然数を求めよ.
長崎県~全国入試問題解法
この動画を見る
各位の数の和が5である4けたの自然数のうち,
大きい方から数えて5番目の自然数を求めよ.
長崎県~全国入試問題解法
【落ち着いて考えて…!】整数:長崎県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \color{red}{2023}$を割り切ることでできる自然数の中で
$ \color{green}{2023}$の$ \color{orange}{次の大きな自然数}$を求めよ.
長崎県公立高等学校過去問
この動画を見る
$ \color{red}{2023}$を割り切ることでできる自然数の中で
$ \color{green}{2023}$の$ \color{orange}{次の大きな自然数}$を求めよ.
長崎県公立高等学校過去問
【3分で別解まで分かる!】図形:長崎県~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
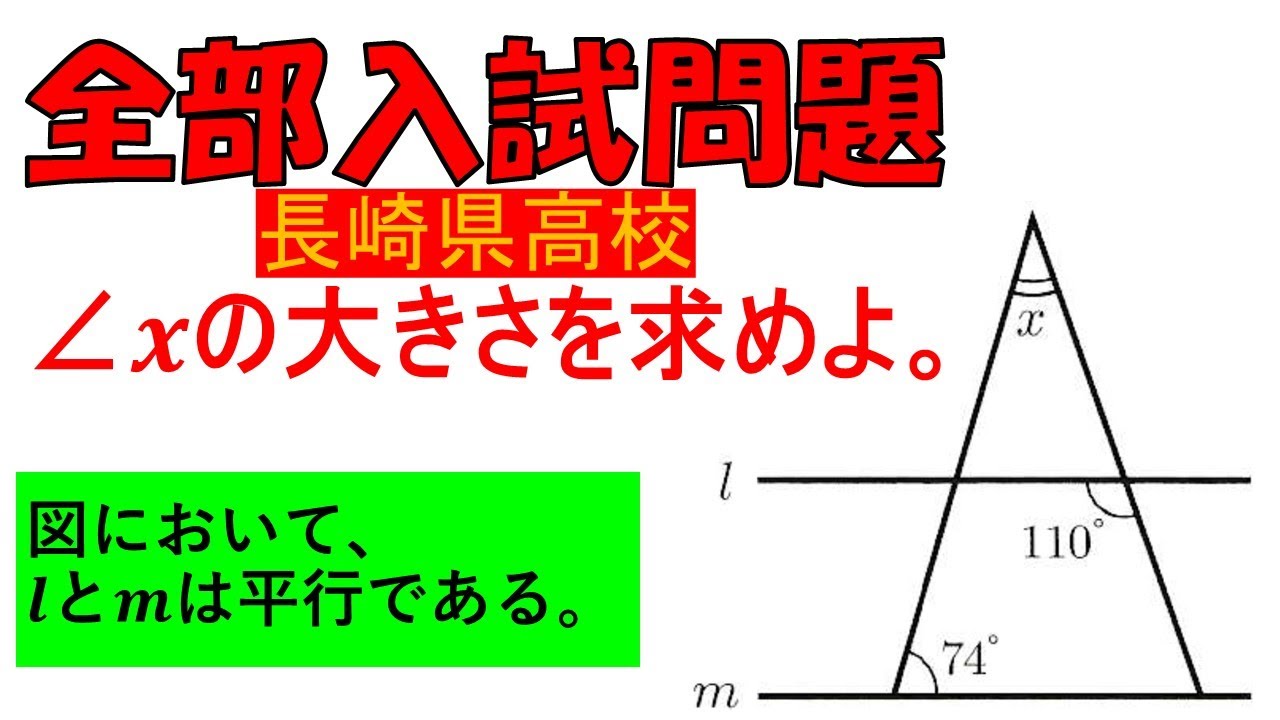
入試問題 長崎県の公立高校
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
この動画を見る
入試問題 長崎県の公立高校
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
【3分間でOK!よく出る!】平方根:長崎県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 長崎県の公立高等学校
$\sqrt{ 67-2n }$
の値が整数に なるような自然数$n$のうち、
最も小さい ものを求めよ。
この動画を見る
入試問題 長崎県の公立高等学校
$\sqrt{ 67-2n }$
の値が整数に なるような自然数$n$のうち、
最も小さい ものを求めよ。
【2分でマスター!】平方根:長崎県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 長崎県の公立高等学校
次の計算をせよ。
$(\sqrt{ 2 }-\sqrt{ 6 })^2+\displaystyle \frac{12}{\sqrt{ 3 }}$
この動画を見る
入試問題 長崎県の公立高等学校
次の計算をせよ。
$(\sqrt{ 2 }-\sqrt{ 6 })^2+\displaystyle \frac{12}{\sqrt{ 3 }}$
