 中3数学
中3数学
 中3数学
中3数学
証明:沖縄県高校入試~全国入試問題解法
単元:
#数学(中学生)#平行と合同#相似な図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
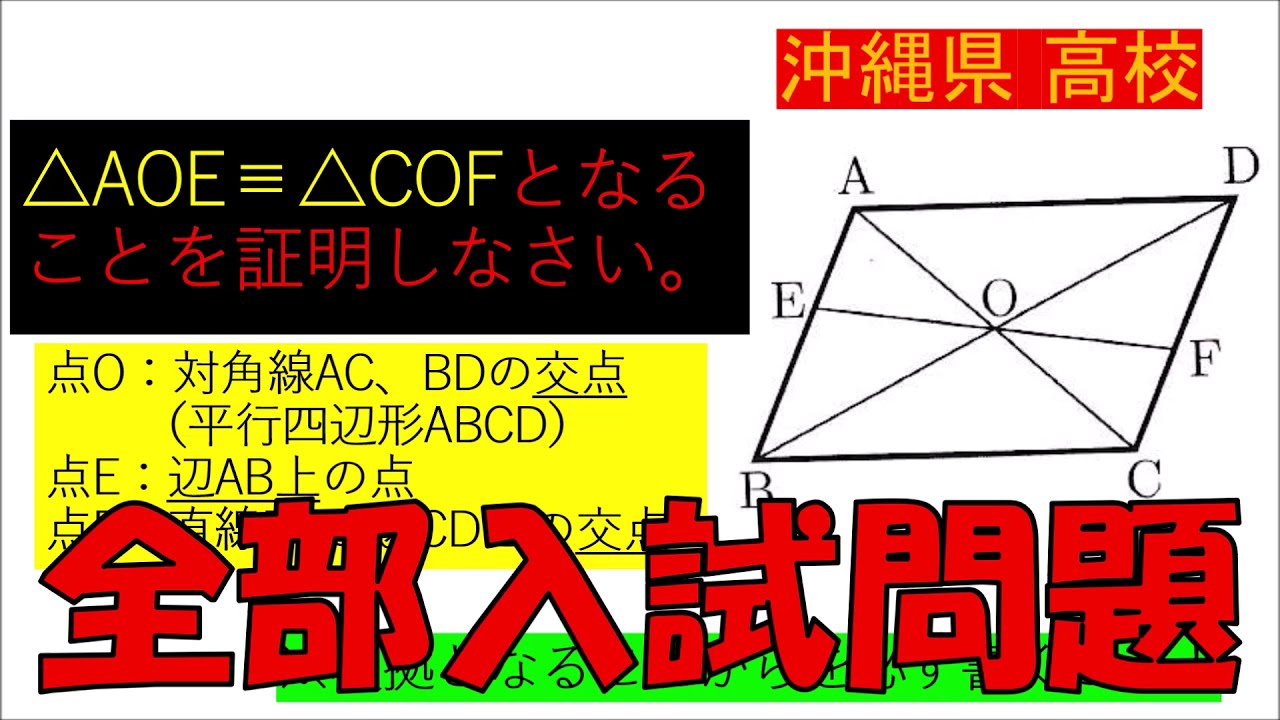
問題文全文(内容文):
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
この動画を見る
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
【中学数学】扇形の中心角の公式~方程式を立てなくても求まる~【中1数学】

変な解き方でごめんなさい。

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$(2021-x)(2022-x) = 2023 - x$
2021慶應義塾高等学校
この動画を見る
2次方程式を解け
$(2021-x)(2022-x) = 2023 - x$
2021慶應義塾高等学校
2021慶應義塾最初の一問 B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
この動画を見る
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
慶應義塾 B 2021最初の一問

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
この動画を見る
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
因数分解 A 中大横浜 2021

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2(x-1)-x+1$を因数分解せよ。
中央大学附属横浜高等学校
この動画を見る
$a^2(x-1)-x+1$を因数分解せよ。
中央大学附属横浜高等学校
二次関数と台形 桃山学院(改) 2021 B

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
台形ABCD=5のときa=?(a>0)
*図は動画内参照
2021桃山学院高等学校
この動画を見る
台形ABCD=5のときa=?(a>0)
*図は動画内参照
2021桃山学院高等学校
2021 慶應志木高校 最初の一題

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a+b+c=0,abc=2021のとき
(ab+ca)(ca+bc)(bc+ab)=
2021慶應義塾志木高等学校
この動画を見る
a+b+c=0,abc=2021のとき
(ab+ca)(ca+bc)(bc+ab)=
2021慶應義塾志木高等学校
因数分解 B 2021 城北
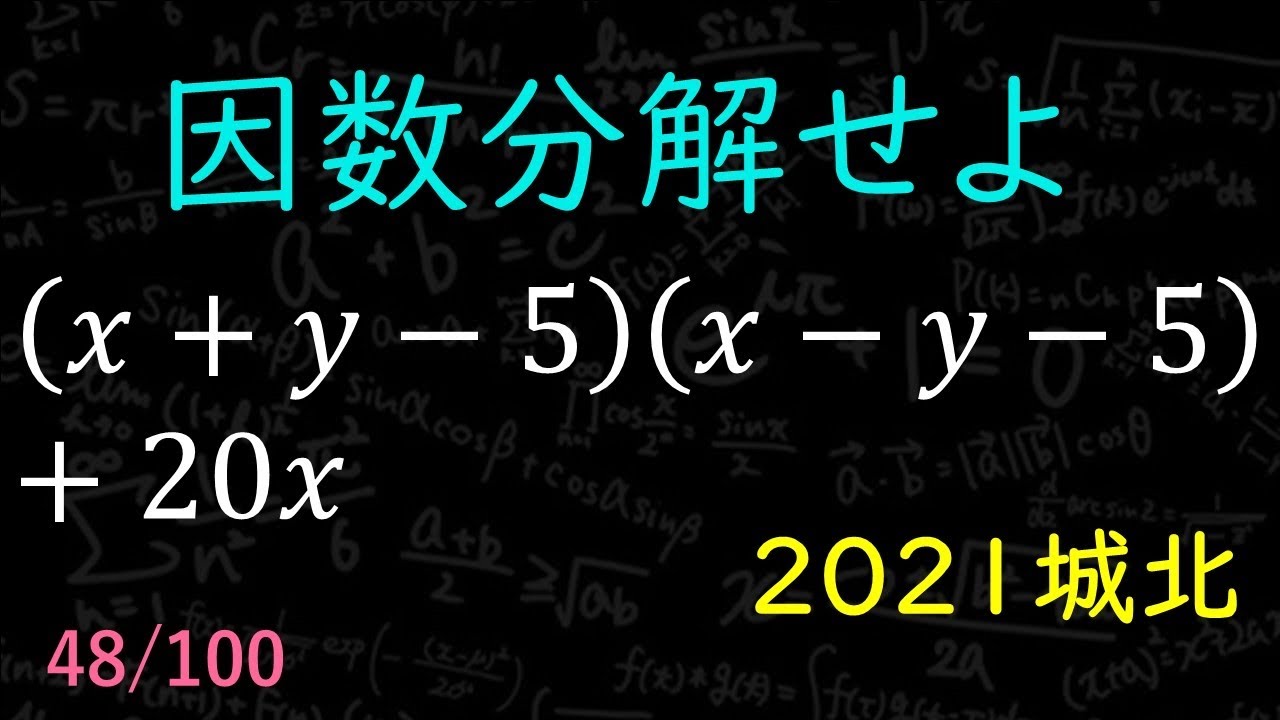
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(x+y-5)(x-y-5)+20xを因数分解せよ。
2021城北高等学校
この動画を見る
(x+y-5)(x-y-5)+20xを因数分解せよ。
2021城北高等学校
誘導に従って因数分解!! 2021中央大学附属 B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$S=n^4-5n^3-10n^2+35n+49$
(1)$(n-\frac{7}{n})^2$を展開せよ。
(2)$t=n-\frac{7}{n}$とするとき$\frac{S}{n^2}$をtで表せ。
(3)Sを因数分解せよ。
2021中央大学附属高等学校
この動画を見る
$S=n^4-5n^3-10n^2+35n+49$
(1)$(n-\frac{7}{n})^2$を展開せよ。
(2)$t=n-\frac{7}{n}$とするとき$\frac{S}{n^2}$をtで表せ。
(3)Sを因数分解せよ。
2021中央大学附属高等学校
因数分解 B 明大明治 2021

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$4a^2-b^2+16c^2-16ac$を因数分解せよ。
2021明治大学付属明治高等学校
この動画を見る
$4a^2-b^2+16c^2-16ac$を因数分解せよ。
2021明治大学付属明治高等学校
【みんな大好き】因数分解:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学付属明治高等学校
$(x-6y+3z)(x+2y-z)+5z(4y-z)-20y^2$
を因数分解すると▭である。
この動画を見る
入試問題 明治大学付属明治高等学校
$(x-6y+3z)(x+2y-z)+5z(4y-z)-20y^2$
を因数分解すると▭である。
平方根の基本 2021久留米信愛学院

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
下線部分は○か✖か
✖なら正せ。
①4の平方根は$\underline{2}$である。
②$\sqrt{16}$は$\underline{4}$である。
③$\sqrt{(-3)^2}$は$\underline{-3}$である。
2021久留米信愛学院高等学校
この動画を見る
下線部分は○か✖か
✖なら正せ。
①4の平方根は$\underline{2}$である。
②$\sqrt{16}$は$\underline{4}$である。
③$\sqrt{(-3)^2}$は$\underline{-3}$である。
2021久留米信愛学院高等学校
そのまま代入すると大変!❓ 2021 城北

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-x-1= 0 $の解のうち大きい方の解をaとする。
$3a^2-a-3=?$
2021城北高等学校
この動画を見る
$x^2-x-1= 0 $の解のうち大きい方の解をaとする。
$3a^2-a-3=?$
2021城北高等学校
【中学数学】扇形の面積と弧の公式~中心角がなくても求まる~【中1数学】

2021 灘高校 2次方程式の応用D
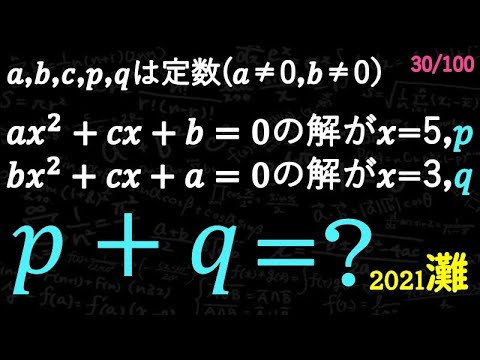
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,c,p,qは定数(a≠0,b≠0)
$ax^2+cx+b=0$の解がx=5,p -①
$bx^2+cx+a=0$の解がx=3,q -②
のときp+q=?
2021灘高等学校
この動画を見る
a,b,c,p,qは定数(a≠0,b≠0)
$ax^2+cx+b=0$の解がx=5,p -①
$bx^2+cx+a=0$の解がx=3,q -②
のときp+q=?
2021灘高等学校
二次方程式:お茶の水女子大附属高校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
二次方程式:お茶の水女子大附属高校~全国入試問題解法
点$A$:①上にあるy=aである点($ a \gt 0$)。
点$B$:$A$を通り$X$軸に平行な直線と②の交点。
点$C$:$A$を通り$X$軸に垂直な直線と②の交点。
$AB=AC$のとき、$a$の値を求めよ。
① :$y=x^2(x \geqq 0)$
② : $y=\displaystyle \frac{1}{4}x^2(x \geqq 0)$
この動画を見る
二次方程式:お茶の水女子大附属高校~全国入試問題解法
点$A$:①上にあるy=aである点($ a \gt 0$)。
点$B$:$A$を通り$X$軸に平行な直線と②の交点。
点$C$:$A$を通り$X$軸に垂直な直線と②の交点。
$AB=AC$のとき、$a$の値を求めよ。
① :$y=x^2(x \geqq 0)$
② : $y=\displaystyle \frac{1}{4}x^2(x \geqq 0)$
二次方程式:渋谷教育学園幕張高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 渋谷教育学園幕張高等学校
共通解をもつとき、その解を求めなさい。
$2x^2-kx-8=0$
$x^2-x-2k = 0$
この動画を見る
入試問題 渋谷教育学園幕張高等学校
共通解をもつとき、その解を求めなさい。
$2x^2-kx-8=0$
$x^2-x-2k = 0$
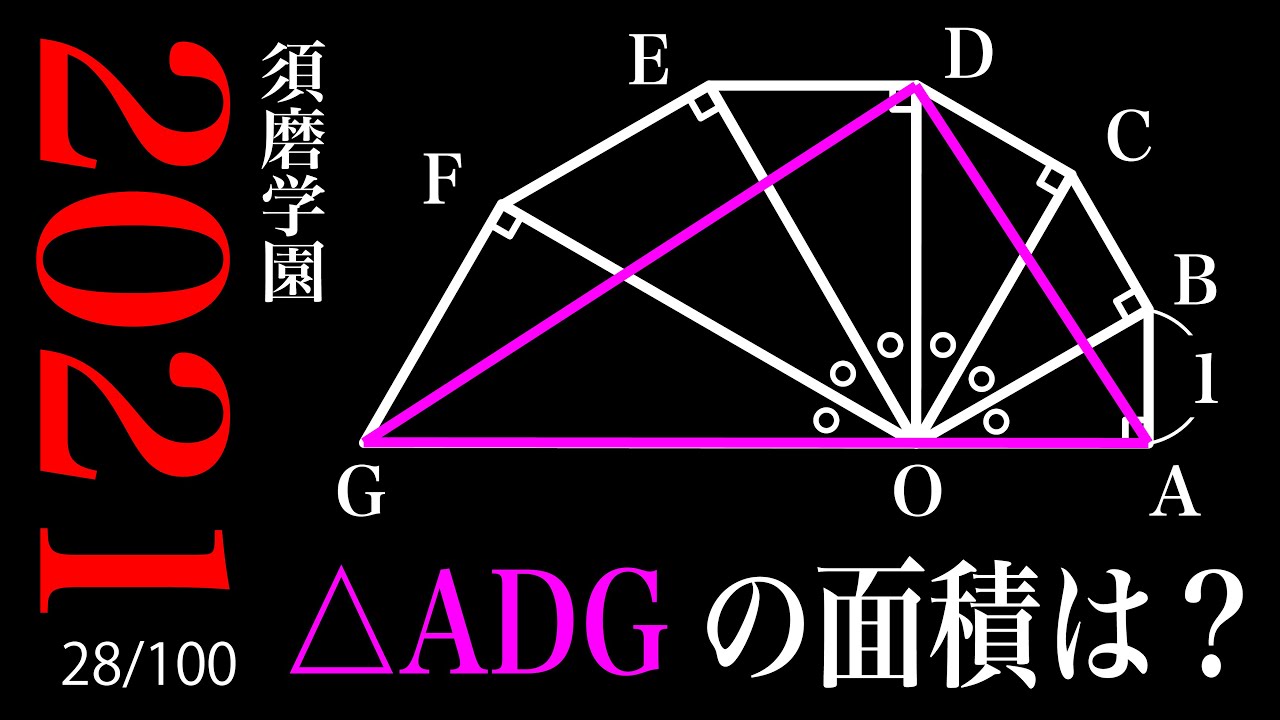
三平方の定理の利用 須磨学園 A
単元:
#数学(中学生)#中3数学#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ADG=?
*図は動画内参照
2021須磨学園高等学校(改)
この動画を見る
△ADG=?
*図は動画内参照
2021須磨学園高等学校(改)
【高校受験対策/数学】文章題9

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・文章題9
Q.
右のカレンダーの中にある3つの日付の数で、次の①~③の関係が成り立つものを求める。
※図は動画参照
①最も小さい数と2番目に小さい数の2つの数は、上下に隣接 している。
②2番目に小さい数と最も大きい数の2つの数は、左右に隣接している。
③最も小さい数の2乗と2番目に小さい数の2乗との和が、最も大きい数の2乗に等しい。
問1
2番目に小さい数を$x$とする。
最も小さい数と最も大きい数を$x$を使った式でそれぞれ表しなさい。
問2
3つの数を求めなさい。
この動画を見る
高校受験対策・文章題9
Q.
右のカレンダーの中にある3つの日付の数で、次の①~③の関係が成り立つものを求める。
※図は動画参照
①最も小さい数と2番目に小さい数の2つの数は、上下に隣接 している。
②2番目に小さい数と最も大きい数の2つの数は、左右に隣接している。
③最も小さい数の2乗と2番目に小さい数の2乗との和が、最も大きい数の2乗に等しい。
問1
2番目に小さい数を$x$とする。
最も小さい数と最も大きい数を$x$を使った式でそれぞれ表しなさい。
問2
3つの数を求めなさい。
2021 東大寺学園 因数分解 B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(3a+2c)(3a-2c)-b(b-4c)-(6a-1)を因数分解せよ。
2021東大寺学園高等学校
この動画を見る
(3a+2c)(3a-2c)-b(b-4c)-(6a-1)を因数分解せよ。
2021東大寺学園高等学校
2021早稲田本庄 平方根の計算B

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\{ (\sqrt 2 - \sqrt 3)^2(5+2\sqrt 6) \}^{2021}
- \{ \frac{(\sqrt 2 -1)^2}{ 2\sqrt 2 -3 } \}^{2021}$
2021早稲田大学 本庄高等学院
この動画を見る
$\{ (\sqrt 2 - \sqrt 3)^2(5+2\sqrt 6) \}^{2021}
- \{ \frac{(\sqrt 2 -1)^2}{ 2\sqrt 2 -3 } \}^{2021}$
2021早稲田大学 本庄高等学院
2021 早稲田本庄最初の一問

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$4(x^2+2xy+y^2) - (2x+y+1)^2$を因数分解せよ。
2021早稲田大学 本庄高等学院
この動画を見る
$4(x^2+2xy+y^2) - (2x+y+1)^2$を因数分解せよ。
2021早稲田大学 本庄高等学院
【高校受験対策/数学】死守70

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・数学 死守70
①$x^2-36y^2$
➁$(x+3)(x-4)-8$
③$(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})$
④$x(x-6)=-4(x-2)$
⑤$3x^2-5x+1=0$
⑥$3a+b=10$
⑦$-6+9÷\frac{1}{4}$
⑧$x^2+xy$
⑨$5xy^2×7xy÷(-x)^2$
➉$\frac{5x-3y}{3}-\frac{3x-7y}{4}$
⑪$3x+4y=x+y=2$
⑫$(2\sqrt{10}-5)(\sqrt{10}+4)$
⑬$x^2-6x-18$
⑭$(x-5)^2-7(x-5)+12$
⑮$0.2(x-2)=x+1.2$
⑯$\frac{x-2}{4}+\frac{2-5x}{6}=1$
この動画を見る
高校受験対策・数学 死守70
①$x^2-36y^2$
➁$(x+3)(x-4)-8$
③$(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})$
④$x(x-6)=-4(x-2)$
⑤$3x^2-5x+1=0$
⑥$3a+b=10$
⑦$-6+9÷\frac{1}{4}$
⑧$x^2+xy$
⑨$5xy^2×7xy÷(-x)^2$
➉$\frac{5x-3y}{3}-\frac{3x-7y}{4}$
⑪$3x+4y=x+y=2$
⑫$(2\sqrt{10}-5)(\sqrt{10}+4)$
⑬$x^2-6x-18$
⑭$(x-5)^2-7(x-5)+12$
⑮$0.2(x-2)=x+1.2$
⑯$\frac{x-2}{4}+\frac{2-5x}{6}=1$
【中学数学】円:点A-Lは、円周を12等分する点である。CKとELの交点をPとするとき、∠CPEの大きさを求めよう。

単元:
#数学(中学生)#中3数学#円
指導講師:
理数個別チャンネル
問題文全文(内容文):
点A-Lは、円周を12等分する点である。CKとELの交点をPとするとき、∠CPEの大きさを求めよう。
この動画を見る
点A-Lは、円周を12等分する点である。CKとELの交点をPとするとき、∠CPEの大きさを求めよう。
相似な図形の面積比 A 専大松戸

単元:
#数学(中学生)#中2数学#中3数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形EBCGの面積=?
*図は動画内参照
2021専修大学松戸高等学校
この動画を見る
四角形EBCGの面積=?
*図は動画内参照
2021専修大学松戸高等学校
因数分解:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
次の問いに答えよ。
$x^2y^2-4x^2-9y^2+36$
を因数分解すると▭である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
次の問いに答えよ。
$x^2y^2-4x^2-9y^2+36$
を因数分解すると▭である。
【高校受験対策/数学】死守69

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守69
①$-3-6$を計算しなさい。
②$7+(-2^3)×4$を計算しなさい。
③$(-3ab)^2÷\frac{6}{5}a^2b$を計算しなさい。
④$\frac{x+3y}{4}-\frac{2x-y}{3}$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2+5x-3=0$
⑦$x=\sqrt{7}+\sqrt{2}$、$y=\sqrt{7}-\sqrt{2}$のとき
$x^2-y^2$の値を求めなさい。
⑧折り紙が$a$枚ある。この折り紙を1人に5枚ずつ$b$人に配ったら 20枚以上余った。
このときの数量の間の関係を、不等式で表しなさい。
⑨太郎さんのクラス生徒全員について、ある期間に図書室から借りた本の冊数を調べ、表にまとめた。
しかし、表の一部が破れてしまい、いくつかの数値がわからなくなった。
このときこのクラスの生徒がある期間に借りた本の冊数の平均値を求めなさい。
➉
$ax+by=11$
$ax-by=-2$
$x$と$y$についての連立方程式の解が$x=3$、$y=-4$であるとき
$a,b$の値を求めなさい。
この動画を見る
高校受験対策・死守69
①$-3-6$を計算しなさい。
②$7+(-2^3)×4$を計算しなさい。
③$(-3ab)^2÷\frac{6}{5}a^2b$を計算しなさい。
④$\frac{x+3y}{4}-\frac{2x-y}{3}$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2+5x-3=0$
⑦$x=\sqrt{7}+\sqrt{2}$、$y=\sqrt{7}-\sqrt{2}$のとき
$x^2-y^2$の値を求めなさい。
⑧折り紙が$a$枚ある。この折り紙を1人に5枚ずつ$b$人に配ったら 20枚以上余った。
このときの数量の間の関係を、不等式で表しなさい。
⑨太郎さんのクラス生徒全員について、ある期間に図書室から借りた本の冊数を調べ、表にまとめた。
しかし、表の一部が破れてしまい、いくつかの数値がわからなくなった。
このときこのクラスの生徒がある期間に借りた本の冊数の平均値を求めなさい。
➉
$ax+by=11$
$ax-by=-2$
$x$と$y$についての連立方程式の解が$x=3$、$y=-4$であるとき
$a,b$の値を求めなさい。
【中学数学】円:点A-Lは、円周を12等分する点である。DIとELの交点をPとするとき、∠DPEの大きさを求めよう。

単元:
#数学(中学生)#中3数学#円
指導講師:
理数個別チャンネル
問題文全文(内容文):
点A-Lは、円周を12等分する点である。DIとELの交点をPとするとき、∠DPEの大きさを求めよう。
この動画を見る
点A-Lは、円周を12等分する点である。DIとELの交点をPとするとき、∠DPEの大きさを求めよう。
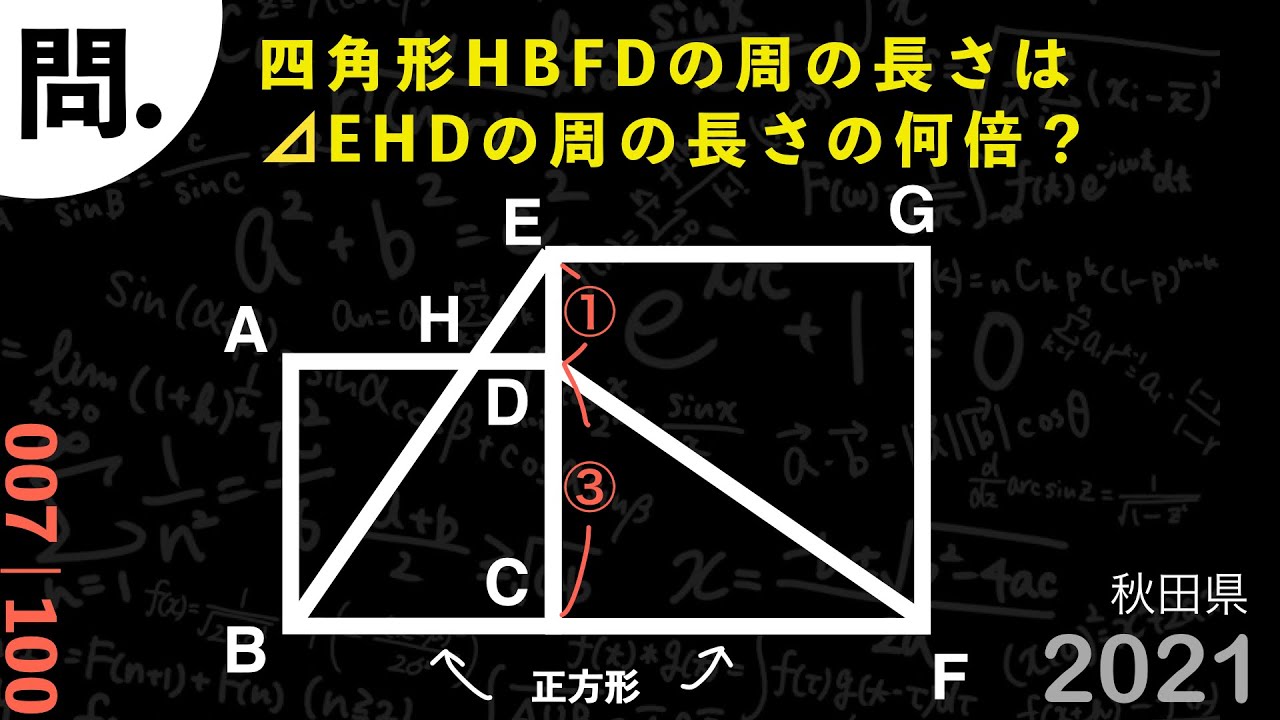
秋田県 2021 相似and三平方 A
単元:
#数学(中学生)#中3数学#相似な図形#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形HBFDの周の長さは△EHDの周の長さの何倍?
*図は動画内参照
2021秋田県
この動画を見る
四角形HBFDの周の長さは△EHDの周の長さの何倍?
*図は動画内参照
2021秋田県
