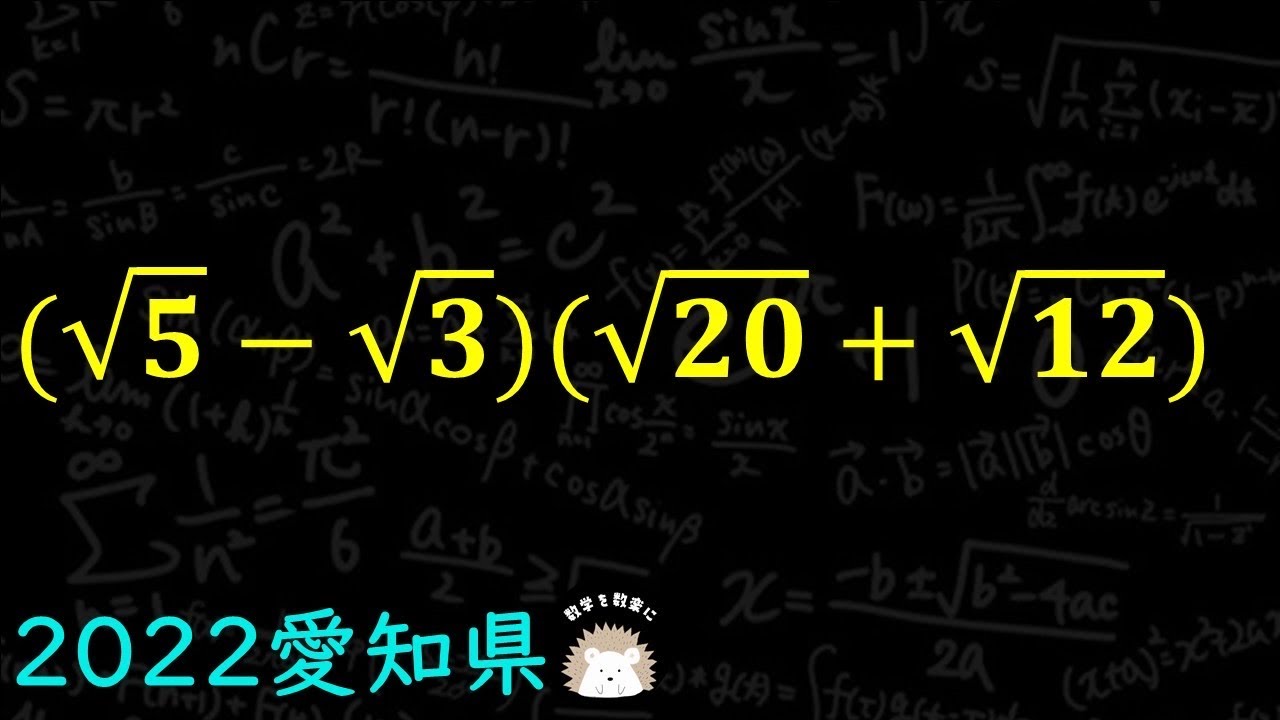問題文全文(内容文):
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
投稿日:2022.07.22