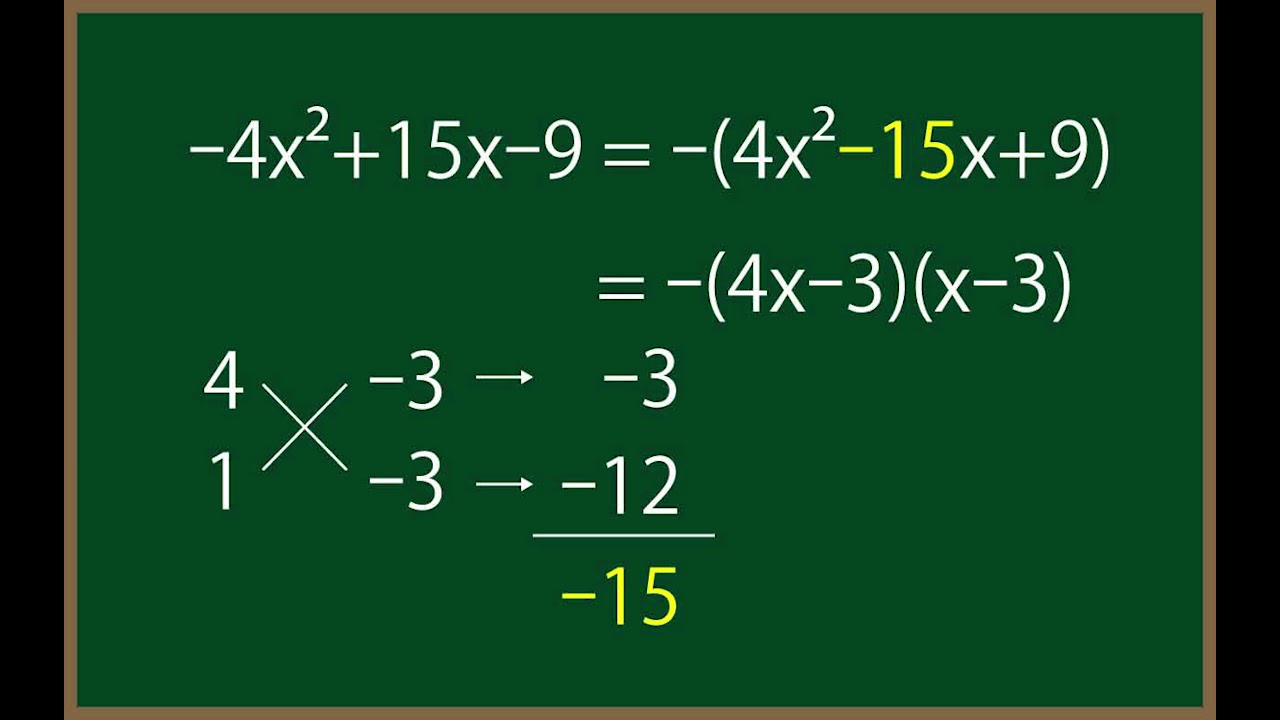問題文全文(内容文):
${\Large\boxed{3}}$ある高校の生徒30人に対し、50m走のタイムを2回計測した。
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果
を縦軸に取った散布図である。
(1)次の$(\textrm{A})$から$(\textrm{F})$のうち、1回目の計測結果の箱ひげ図
として適当なものは$\boxed{\ \ ネ\ \ }$であり、2回目の計測結果の箱ひげ図として
適当なものは$\boxed{\ \ ノ\ \ }$である。
(2)次の$(\textrm{G})$から$(\textrm{L})$のうち、1回目と2回目の計測結果の合計の
箱ひげ図として適切なものは$\boxed{\ \ ハ\ \ }$である。
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を$\bar{ x_{31} }$,中央値を
$m_{31}$とする。$\bar{ x_{30} }=17.0$であることに注意すると、
$\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }$である。一方、
$m_{31}-m_{30}=\boxed{\ \ フ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
${\Large\boxed{3}}$ある高校の生徒30人に対し、50m走のタイムを2回計測した。
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果
を縦軸に取った散布図である。
(1)次の$(\textrm{A})$から$(\textrm{F})$のうち、1回目の計測結果の箱ひげ図
として適当なものは$\boxed{\ \ ネ\ \ }$であり、2回目の計測結果の箱ひげ図として
適当なものは$\boxed{\ \ ノ\ \ }$である。
(2)次の$(\textrm{G})$から$(\textrm{L})$のうち、1回目と2回目の計測結果の合計の
箱ひげ図として適切なものは$\boxed{\ \ ハ\ \ }$である。
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を$\bar{ x_{31} }$,中央値を
$m_{31}$とする。$\bar{ x_{30} }=17.0$であることに注意すると、
$\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }$である。一方、
$m_{31}-m_{30}=\boxed{\ \ フ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ある高校の生徒30人に対し、50m走のタイムを2回計測した。
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果
を縦軸に取った散布図である。
(1)次の$(\textrm{A})$から$(\textrm{F})$のうち、1回目の計測結果の箱ひげ図
として適当なものは$\boxed{\ \ ネ\ \ }$であり、2回目の計測結果の箱ひげ図として
適当なものは$\boxed{\ \ ノ\ \ }$である。
(2)次の$(\textrm{G})$から$(\textrm{L})$のうち、1回目と2回目の計測結果の合計の
箱ひげ図として適切なものは$\boxed{\ \ ハ\ \ }$である。
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を$\bar{ x_{31} }$,中央値を
$m_{31}$とする。$\bar{ x_{30} }=17.0$であることに注意すると、
$\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }$である。一方、
$m_{31}-m_{30}=\boxed{\ \ フ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
${\Large\boxed{3}}$ある高校の生徒30人に対し、50m走のタイムを2回計測した。
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果
を縦軸に取った散布図である。
(1)次の$(\textrm{A})$から$(\textrm{F})$のうち、1回目の計測結果の箱ひげ図
として適当なものは$\boxed{\ \ ネ\ \ }$であり、2回目の計測結果の箱ひげ図として
適当なものは$\boxed{\ \ ノ\ \ }$である。
(2)次の$(\textrm{G})$から$(\textrm{L})$のうち、1回目と2回目の計測結果の合計の
箱ひげ図として適切なものは$\boxed{\ \ ハ\ \ }$である。
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を$\bar{ x_{31} }$,中央値を
$m_{31}$とする。$\bar{ x_{30} }=17.0$であることに注意すると、
$\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }$である。一方、
$m_{31}-m_{30}=\boxed{\ \ フ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
投稿日:2021.08.09