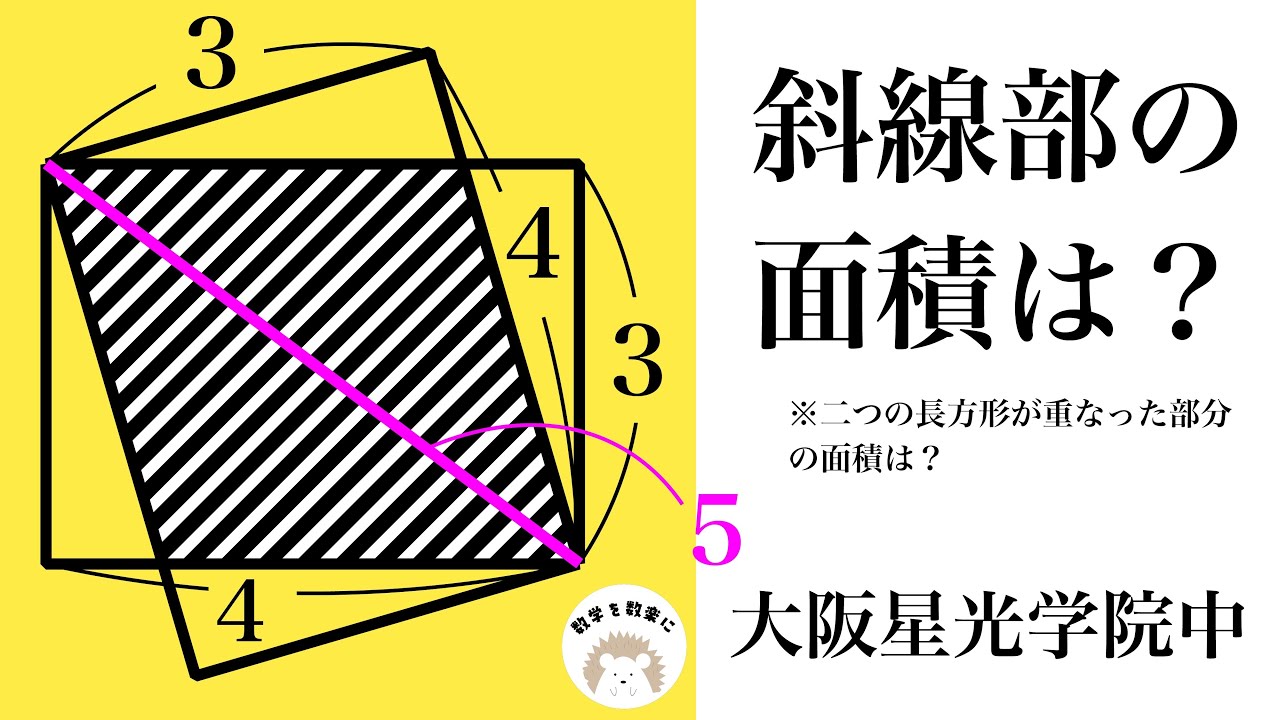
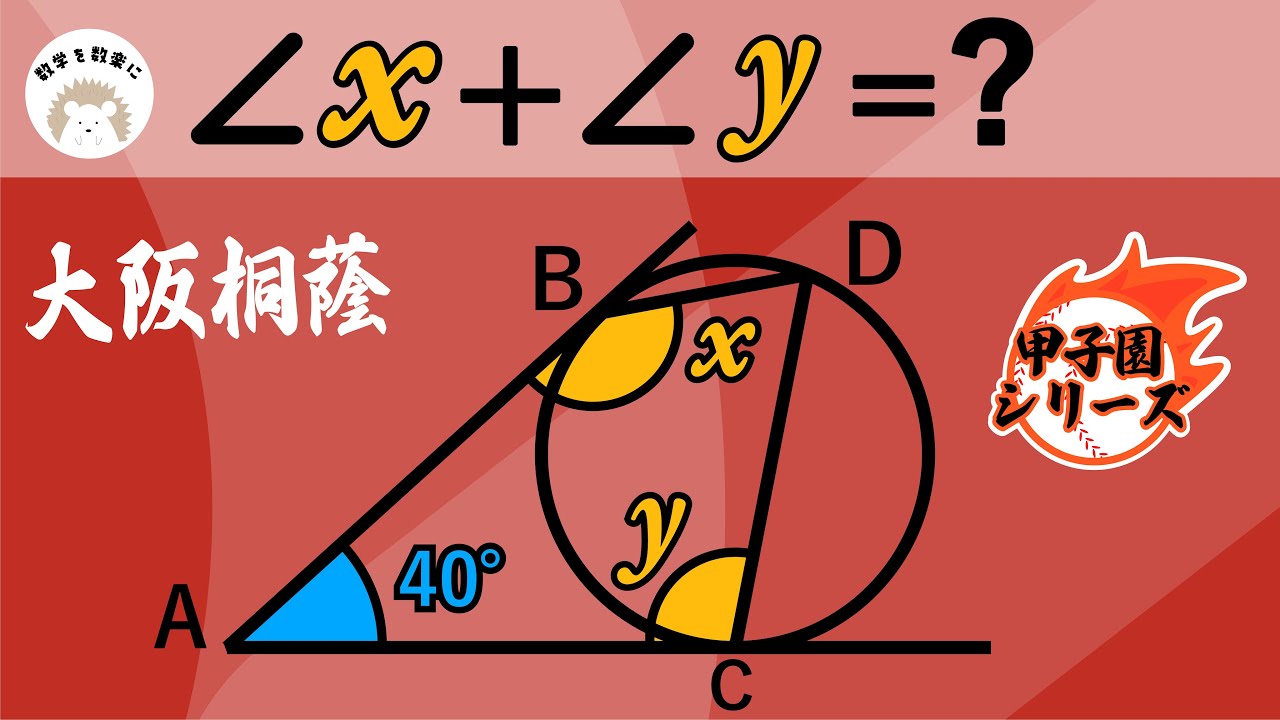
問題文全文(内容文):
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
投稿日:2023.08.16