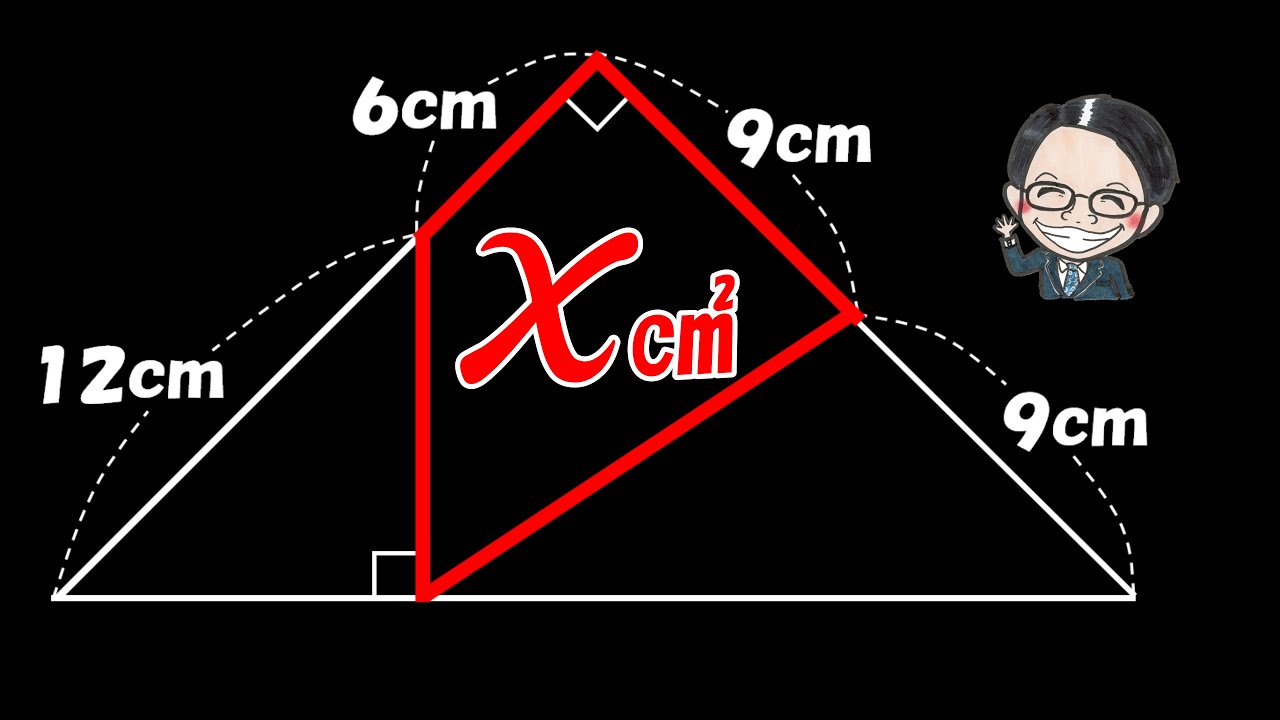
問題文全文(内容文):
算数(時こくと時間は何がちがうの?)
ポイント
好きなテレビ番組は(午後6時)から始まって、(30分間)放送される
①家から学校まで歩くと40分かかります。
家を7時30分に出るとき学校に着く時こくは何時何分ですか。
②ぼくの家から公園まで15分かかります。
公園に2時40分に着くには、家を何時何分に出ればいいかな。
算数(時こくと時間は何がちがうの?)
ポイント
好きなテレビ番組は(午後6時)から始まって、(30分間)放送される
①家から学校まで歩くと40分かかります。
家を7時30分に出るとき学校に着く時こくは何時何分ですか。
②ぼくの家から公園まで15分かかります。
公園に2時40分に着くには、家を何時何分に出ればいいかな。
単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(時こくと時間は何がちがうの?)
ポイント
好きなテレビ番組は(午後6時)から始まって、(30分間)放送される
①家から学校まで歩くと40分かかります。
家を7時30分に出るとき学校に着く時こくは何時何分ですか。
②ぼくの家から公園まで15分かかります。
公園に2時40分に着くには、家を何時何分に出ればいいかな。
算数(時こくと時間は何がちがうの?)
ポイント
好きなテレビ番組は(午後6時)から始まって、(30分間)放送される
①家から学校まで歩くと40分かかります。
家を7時30分に出るとき学校に着く時こくは何時何分ですか。
②ぼくの家から公園まで15分かかります。
公園に2時40分に着くには、家を何時何分に出ればいいかな。
投稿日:2022.05.10