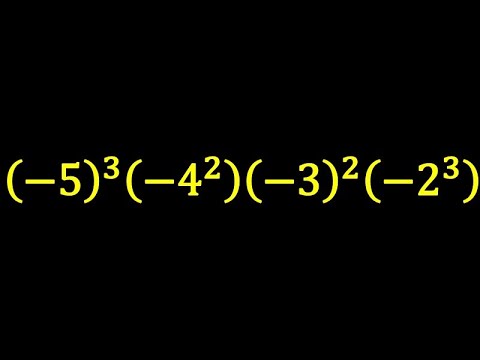問題文全文(内容文):
$\boxed{1}$
(1)$2(a+4b)+3(a-2b)$を計算せよ.
(2)$\sqrt{27}-\dfrac{6}{\sqrt3}$を計算せよ.
(3)$(x+1)^2+(x-4)(x+2)$を計算せよ.
(4)袋の中に赤玉2個と白玉1個.この袋から玉を1個取り出し,色を調べて戻す.
もう1度玉を取り出すとき,2個共赤玉が出る確率を求めよ.
$\boxed{2}$
(1)$a$の値は?
(2)点$c$の$y$座標
(3)$\triangle ABC$の面積は?
(4)2点$A,B$を通る直線の式は?
$\boxed{3}$
(1)$\triangle AFC \equiv \triangle BEC$の証明をせよ.
(2)$\triangle=40cm^2$のとき,$\triangle ABF=20cm^2$のとき,$AF=?$
山形県立高校過去問
$\boxed{1}$
(1)$2(a+4b)+3(a-2b)$を計算せよ.
(2)$\sqrt{27}-\dfrac{6}{\sqrt3}$を計算せよ.
(3)$(x+1)^2+(x-4)(x+2)$を計算せよ.
(4)袋の中に赤玉2個と白玉1個.この袋から玉を1個取り出し,色を調べて戻す.
もう1度玉を取り出すとき,2個共赤玉が出る確率を求めよ.
$\boxed{2}$
(1)$a$の値は?
(2)点$c$の$y$座標
(3)$\triangle ABC$の面積は?
(4)2点$A,B$を通る直線の式は?
$\boxed{3}$
(1)$\triangle AFC \equiv \triangle BEC$の証明をせよ.
(2)$\triangle=40cm^2$のとき,$\triangle ABF=20cm^2$のとき,$AF=?$
山形県立高校過去問
単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#確率#2次関数#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$2(a+4b)+3(a-2b)$を計算せよ.
(2)$\sqrt{27}-\dfrac{6}{\sqrt3}$を計算せよ.
(3)$(x+1)^2+(x-4)(x+2)$を計算せよ.
(4)袋の中に赤玉2個と白玉1個.この袋から玉を1個取り出し,色を調べて戻す.
もう1度玉を取り出すとき,2個共赤玉が出る確率を求めよ.
$\boxed{2}$
(1)$a$の値は?
(2)点$c$の$y$座標
(3)$\triangle ABC$の面積は?
(4)2点$A,B$を通る直線の式は?
$\boxed{3}$
(1)$\triangle AFC \equiv \triangle BEC$の証明をせよ.
(2)$\triangle=40cm^2$のとき,$\triangle ABF=20cm^2$のとき,$AF=?$
山形県立高校過去問
$\boxed{1}$
(1)$2(a+4b)+3(a-2b)$を計算せよ.
(2)$\sqrt{27}-\dfrac{6}{\sqrt3}$を計算せよ.
(3)$(x+1)^2+(x-4)(x+2)$を計算せよ.
(4)袋の中に赤玉2個と白玉1個.この袋から玉を1個取り出し,色を調べて戻す.
もう1度玉を取り出すとき,2個共赤玉が出る確率を求めよ.
$\boxed{2}$
(1)$a$の値は?
(2)点$c$の$y$座標
(3)$\triangle ABC$の面積は?
(4)2点$A,B$を通る直線の式は?
$\boxed{3}$
(1)$\triangle AFC \equiv \triangle BEC$の証明をせよ.
(2)$\triangle=40cm^2$のとき,$\triangle ABF=20cm^2$のとき,$AF=?$
山形県立高校過去問
投稿日:2022.02.17