 式の計算(単項式・多項式・式の四則計算)
式の計算(単項式・多項式・式の四則計算)
 式の計算(単項式・多項式・式の四則計算)
式の計算(単項式・多項式・式の四則計算)
分数式の計算
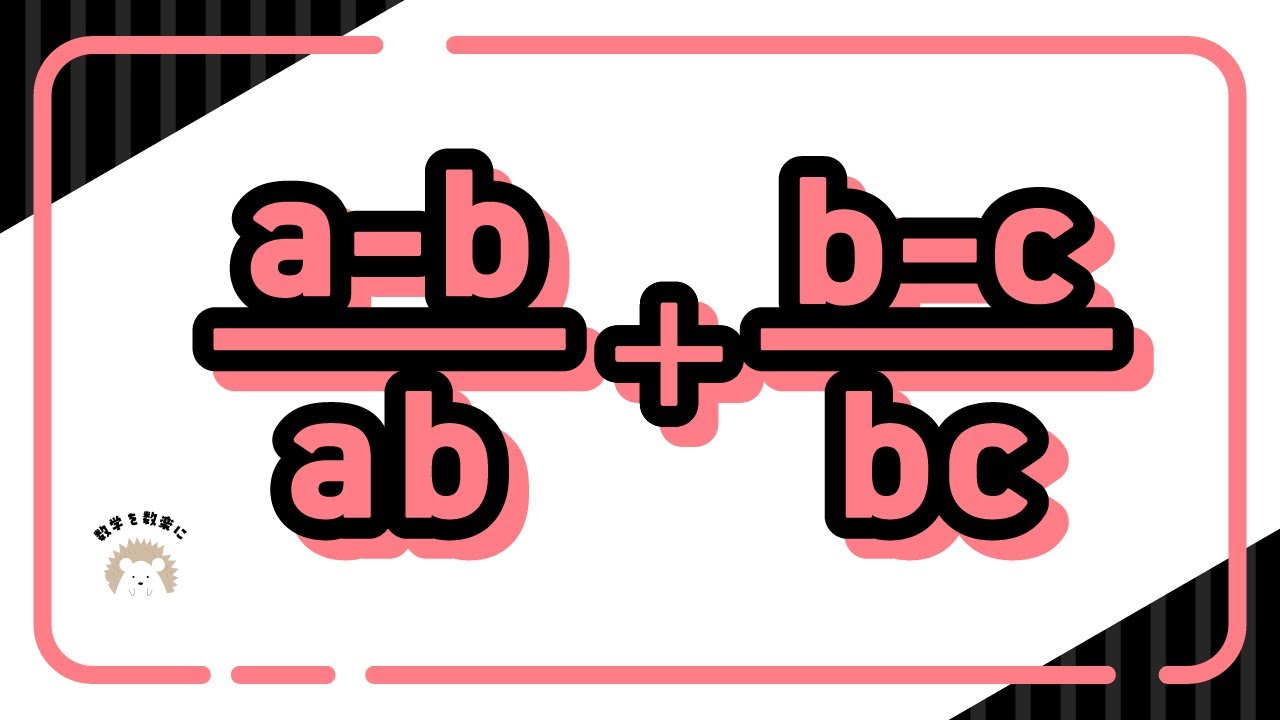
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{a-b}{ab}$+$\frac{b-c}{bc}$
この動画を見る
$\frac{a-b}{ab}$+$\frac{b-c}{bc}$
式の値 2通りで解説
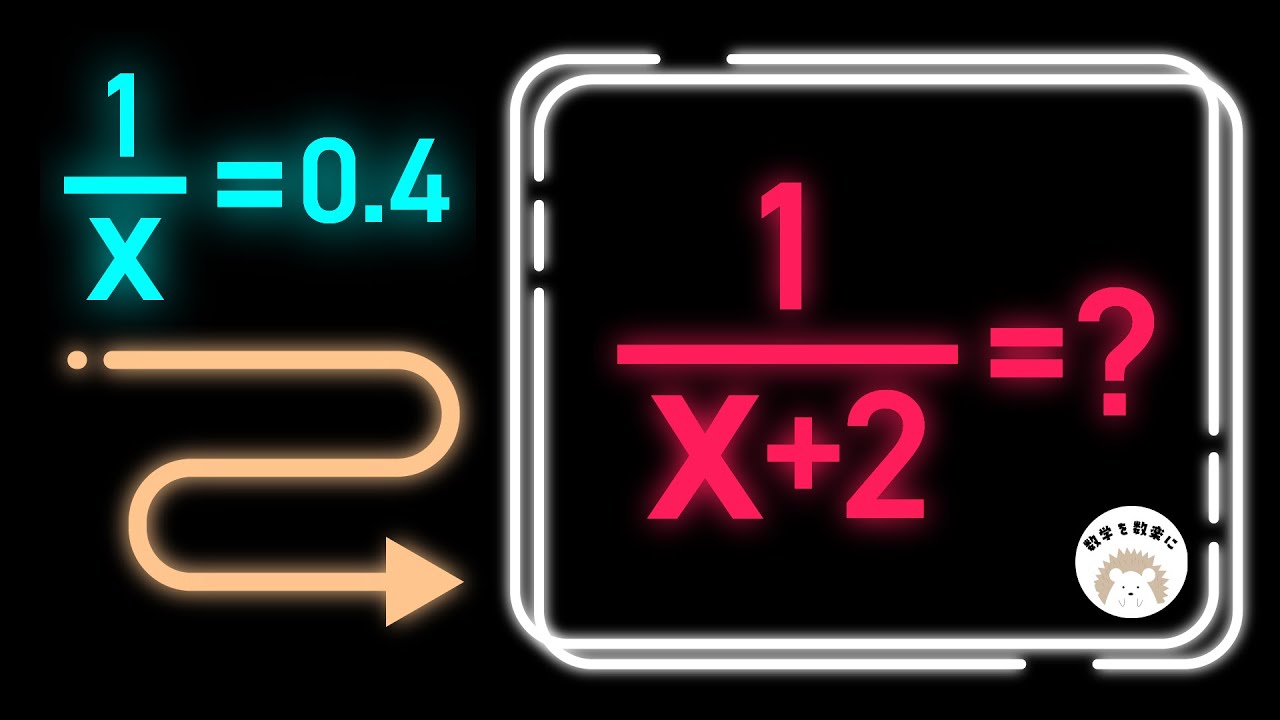
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{x}=0.4$のとき$\frac{1}{x+2}=$
この動画を見る
$\frac{1}{x}=0.4$のとき$\frac{1}{x+2}=$
気付けば一瞬!!式の値 受験生よ。努力が実ることを証明せよ。
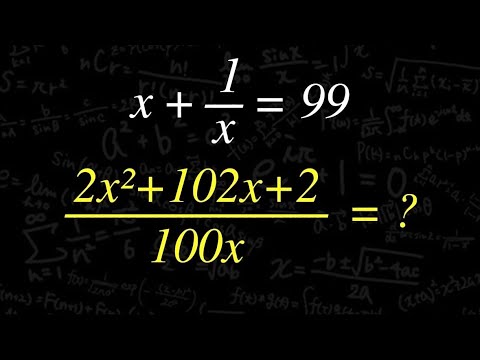
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+\frac{1}{x}=99$のとき
$\frac{2x^2+102x+2}{100x}$の値は?
この動画を見る
$x+\frac{1}{x}=99$のとき
$\frac{2x^2+102x+2}{100x}$の値は?
【本当に解はあるのか!?】整数:日本大学習志野高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#高校入試過去問(数学)#日本大学習志野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3つの自然数$ x,y,z(x \lt y \lt z)$である.
$ x+y+z=20 $
$ xyz=60 $ 満たす.
このとき, $ x=\Box,y=\Box,z=\Box $
日大習志野高校過去問
この動画を見る
3つの自然数$ x,y,z(x \lt y \lt z)$である.
$ x+y+z=20 $
$ xyz=60 $ 満たす.
このとき, $ x=\Box,y=\Box,z=\Box $
日大習志野高校過去問
【中学数学】数学用語チェック絵本 中2の用語”せめて”これだけは覚えよう!!act2まとめ

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#資料の活用#1次関数#平行と合同#確率#三角形と四角形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
この動画を見る
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
【ひるまず進め!】計算:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(1.2\div 0.375+\dfrac{-2^3}{3}\times 4.2\right)\div \left(-\dfrac{2}{3}\right)^3$を計算しなさい.
法政大高校過去問
この動画を見る
$ \left(1.2\div 0.375+\dfrac{-2^3}{3}\times 4.2\right)\div \left(-\dfrac{2}{3}\right)^3$を計算しなさい.
法政大高校過去問
【ルールを抑えるのが大切!】文字式:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{2x+5y}{3}-\dfrac{x+7y}{6}\right)\div \dfrac{xy}{2}$を計算し,簡単にすると$ \Box $である.
福岡大学附属大濠高等学校過去問
この動画を見る
$ \left(\dfrac{2x+5y}{3}-\dfrac{x+7y}{6}\right)\div \dfrac{xy}{2}$を計算し,簡単にすると$ \Box $である.
福岡大学附属大濠高等学校過去問
【中学数学】数学用語チェック絵本 act2 vol.1 式の計算

【中学数学】中学数学:数学検定3級2次:問題1・2

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#数学検定・数学甲子園・数学オリンピック等#空間図形#文字と式#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
① 2ab + c² > 150 ② 2ab + c² ≧ 150 ③ 2ab + c² < 150
④ 2ab + c² ≦ 150 ⑤ a²b²+ c² < 150 ⑥ a²b²+ c² ≦ 150
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
この動画を見る
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
① 2ab + c² > 150 ② 2ab + c² ≧ 150 ③ 2ab + c² < 150
④ 2ab + c² ≦ 150 ⑤ a²b²+ c² < 150 ⑥ a²b²+ c² ≦ 150
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
中学生向け整数問題その3

単元:
#中2数学#式の計算(単項式・多項式・式の四則計算)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 自然数A,Bの最大公約数が6で最小公倍数は432である.(A,B)をすべて求めよ.$
この動画を見る
$ 自然数A,Bの最大公約数が6で最小公倍数は432である.(A,B)をすべて求めよ.$
みんなの説明も聞きたいです…

【中学数学】多項式の乗法除法の問題演習~計算ミスしない方法~ 1-4【中2数学】

【中学数学】多項式の加法減法の問題演習~計算ミスしない方法~ 1-3【中2数学】

【数学検定】数学検定3級対策問題1

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#数学検定・数学甲子園・数学オリンピック等#文字と式#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
数学検定3級対策問題1の解説動画です。
問題1.次の計算をしなさい。
(1) 9-(-5)+(-8)
(2) 24-16÷(-4)
(3) 2³+(-3)²
(4) 35/36 ÷ (-2/9) × 4/7
(5) √125-√45+√20
(6) (√3+4)²-24/√3
(7) 3(3x+5)+4(2x-7)
(8) 0.5(6x-1)-0.8(3x-4)
(9) 7(4x-5y)-2(9x+y)
(10) 3x-6y/8 - 2x-7y/12
(11) -5x²y × 9x²y²
(12) 13x³y²/5 ÷ (-4x²y/5) × (-2xy²/13)
この動画を見る
数学検定3級対策問題1の解説動画です。
問題1.次の計算をしなさい。
(1) 9-(-5)+(-8)
(2) 24-16÷(-4)
(3) 2³+(-3)²
(4) 35/36 ÷ (-2/9) × 4/7
(5) √125-√45+√20
(6) (√3+4)²-24/√3
(7) 3(3x+5)+4(2x-7)
(8) 0.5(6x-1)-0.8(3x-4)
(9) 7(4x-5y)-2(9x+y)
(10) 3x-6y/8 - 2x-7y/12
(11) -5x²y × 9x²y²
(12) 13x³y²/5 ÷ (-4x²y/5) × (-2xy²/13)
【簡潔に予習・復習!】多項式(式の利用):教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
【簡潔に予習・復習!】多項式(後編):式の展開と因数分解~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
【簡潔に予習・復習!】多項式(前編):教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
【何を問われているか理解しているか?】計算:鎌倉学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をしなさい.
${{2^3-(-2)^3}}\times{-2^5+(-2)^5}$
鎌倉学園高校過去問
この動画を見る
次の計算をしなさい.
${{2^3-(-2)^3}}\times{-2^5+(-2)^5}$
鎌倉学園高校過去問
動体視力と数学を鍛えるサウンド~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の$\Box$をうめなさい.
$624^2-623\times625=\Box$
土浦日大高校過去問
この動画を見る
次の$\Box$をうめなさい.
$624^2-623\times625=\Box$
土浦日大高校過去問
【6分でマスター!!】単項式と多項式の次数の求め方を解説!(係数と定数項についても)〔現役塾講師解説、数学〕

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
単項式と多項式の次数の求め方について解説します。
この動画を見る
数学1A
単項式と多項式の次数の求め方について解説します。
【中学数学】式の値~問題演習で解き方を教えます~ 1-2【中2数学】

中2数学「式による説明④(カレンダー問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~第10回式による説明④(カレンダー問題)
(1)枠Aのように、 縦に並んだ3つの数の和は、 真ん中の数の3倍にな ることを説明しなさい。
この動画を見る
中2~第10回式による説明④(カレンダー問題)
(1)枠Aのように、 縦に並んだ3つの数の和は、 真ん中の数の3倍にな ることを説明しなさい。
【中学数学】多項式の計算~単項式・多項式・次数・定数項・同類項~ 1-1【中2数学】

高等学校入試予想問題:富山県~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平行と合同#文字と式#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$6a^2b\times 2b\div 3ab$を計算せよ.
(2)$\sqrt{32}-\sqrt{18}+\sqrt2$を計算せよ.
(3)$x^2-5x-24=0$を解け.
(4)「$am$のリボンから.$bcm$切り取ると残りの長さは$2m$より短い.」
不等式で表せ.
(5)$\angle x$は何度か.
$\boxed{2}$
(1)7番目の図形と16番目の図形の面積をそれぞれ求めよ.
(2)$n$を偶数とするとき,$n$番目の図形と$(2n+1)$番目の図形の面積の差が$331cm^2$である.$n$はいくつか.
$boxed{3}$
$A,B,C,D,E$は円$O$上の5点である.
$AC,BD$は直径であり,$AD\parallel BD$,交点は$F,G$である.
(1)$CE=?,OG=?$
(2)$FG=?$
(3)$\triangle ACF$と$\triangle ODA$の面積比は?
この動画を見る
$\boxed{1}$
(1)$6a^2b\times 2b\div 3ab$を計算せよ.
(2)$\sqrt{32}-\sqrt{18}+\sqrt2$を計算せよ.
(3)$x^2-5x-24=0$を解け.
(4)「$am$のリボンから.$bcm$切り取ると残りの長さは$2m$より短い.」
不等式で表せ.
(5)$\angle x$は何度か.
$\boxed{2}$
(1)7番目の図形と16番目の図形の面積をそれぞれ求めよ.
(2)$n$を偶数とするとき,$n$番目の図形と$(2n+1)$番目の図形の面積の差が$331cm^2$である.$n$はいくつか.
$boxed{3}$
$A,B,C,D,E$は円$O$上の5点である.
$AC,BD$は直径であり,$AD\parallel BD$,交点は$F,G$である.
(1)$CE=?,OG=?$
(2)$FG=?$
(3)$\triangle ACF$と$\triangle ODA$の面積比は?
高等学校入試予想問題:宮崎県~全国入試問題解法

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#1次関数#確率#2次関数#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$27xy\times x^2\div(-9x^2y)$を計算せよ.
(2)$3(x+6y)-2(x+8y)$を計算せよ.
(3)$y$は$x$に比例し,$x=-3$のとき,$y=36$である.
このとき,$y$を$x$の式で表せ.
(4)箱の中に4本のくじ,そのうち3本が当たり.
Aさんが1本引いて戻す.同様にBさんが引く.
2人共,当たりくじをひく確率は?
$\boxed{2}$
$y=x^2$上に$A(2,4)$である.
点$B$は$y$軸上,$y$座標が4より大きい範囲で動く.
$C,D$は,$B$を通り,$x$軸と平行な直線と$y=x^2$の交点である.
(1)点$E$の$x$座標が5となるとき,$\triangle AOE$の面積は?
(2)$CA=AE$となるとき,直線$DE$の傾きは?
$\boxed{3}$
(1)$\triangle AED \backsim \triangle CFD$であることの証明をせよ.
(2)$AE=&,EB=5,BC=2,CF=8$のとき,
①$AC=?$ ②$AD=?$ ③$DF=?$ ④$\Box ABFD$の面積は?
この動画を見る
$\boxed{1}$
(1)$27xy\times x^2\div(-9x^2y)$を計算せよ.
(2)$3(x+6y)-2(x+8y)$を計算せよ.
(3)$y$は$x$に比例し,$x=-3$のとき,$y=36$である.
このとき,$y$を$x$の式で表せ.
(4)箱の中に4本のくじ,そのうち3本が当たり.
Aさんが1本引いて戻す.同様にBさんが引く.
2人共,当たりくじをひく確率は?
$\boxed{2}$
$y=x^2$上に$A(2,4)$である.
点$B$は$y$軸上,$y$座標が4より大きい範囲で動く.
$C,D$は,$B$を通り,$x$軸と平行な直線と$y=x^2$の交点である.
(1)点$E$の$x$座標が5となるとき,$\triangle AOE$の面積は?
(2)$CA=AE$となるとき,直線$DE$の傾きは?
$\boxed{3}$
(1)$\triangle AED \backsim \triangle CFD$であることの証明をせよ.
(2)$AE=&,EB=5,BC=2,CF=8$のとき,
①$AC=?$ ②$AD=?$ ③$DF=?$ ④$\Box ABFD$の面積は?
高等学校入試予想問題:山形県~全国入試問題解法

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#確率#2次関数#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$2(a+4b)+3(a-2b)$を計算せよ.
(2)$\sqrt{27}-\dfrac{6}{\sqrt3}$を計算せよ.
(3)$(x+1)^2+(x-4)(x+2)$を計算せよ.
(4)袋の中に赤玉2個と白玉1個.この袋から玉を1個取り出し,色を調べて戻す.
もう1度玉を取り出すとき,2個共赤玉が出る確率を求めよ.
$\boxed{2}$
(1)$a$の値は?
(2)点$c$の$y$座標
(3)$\triangle ABC$の面積は?
(4)2点$A,B$を通る直線の式は?
$\boxed{3}$
(1)$\triangle AFC \equiv \triangle BEC$の証明をせよ.
(2)$\triangle=40cm^2$のとき,$\triangle ABF=20cm^2$のとき,$AF=?$
山形県立高校過去問
この動画を見る
$\boxed{1}$
(1)$2(a+4b)+3(a-2b)$を計算せよ.
(2)$\sqrt{27}-\dfrac{6}{\sqrt3}$を計算せよ.
(3)$(x+1)^2+(x-4)(x+2)$を計算せよ.
(4)袋の中に赤玉2個と白玉1個.この袋から玉を1個取り出し,色を調べて戻す.
もう1度玉を取り出すとき,2個共赤玉が出る確率を求めよ.
$\boxed{2}$
(1)$a$の値は?
(2)点$c$の$y$座標
(3)$\triangle ABC$の面積は?
(4)2点$A,B$を通る直線の式は?
$\boxed{3}$
(1)$\triangle AFC \equiv \triangle BEC$の証明をせよ.
(2)$\triangle=40cm^2$のとき,$\triangle ABF=20cm^2$のとき,$AF=?$
山形県立高校過去問
高等学校入学試験問題予想:岐阜県~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#平行と合同#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$4+10\div(-2)$を計算せよ.
(2)$2(4x-y)-(7x-5y)$を計算せよ.
(3)$6ab\div 2a\times b$を計算せよ.
(4)次の数を大きい順に左から並べなさい.
$2\sqrt2,\sqrt7,3$
$\boxed{2}$
(1)$\angle GHF=?$
(2)$\triangle GHF \backsim \triangle FDE$の証明
(3)$AG=3cm,GF=5cm$のとき,$HF=?,AB=?,\triangle FDE=?$
岐阜県立高校過去問
この動画を見る
$\boxed{1}$
(1)$4+10\div(-2)$を計算せよ.
(2)$2(4x-y)-(7x-5y)$を計算せよ.
(3)$6ab\div 2a\times b$を計算せよ.
(4)次の数を大きい順に左から並べなさい.
$2\sqrt2,\sqrt7,3$
$\boxed{2}$
(1)$\angle GHF=?$
(2)$\triangle GHF \backsim \triangle FDE$の証明
(3)$AG=3cm,GF=5cm$のとき,$HF=?,AB=?,\triangle FDE=?$
岐阜県立高校過去問
3=4になるらしい~0で割ったらダメな理由~

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
3=4 0で割ったらダメな理由説明動画です
この動画を見る
3=4 0で割ったらダメな理由説明動画です
中2数学「式による説明③(2けたの自然数)」【毎日配信】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~第10回式による説明③~ (2けたの自然数)
例題
2けたの自然数と、その数の十の位の数と一の位の数を入れかえでできる数 との和が11の倍数になる ことを 説明しなさ い。
この動画を見る
中2~第10回式による説明③~ (2けたの自然数)
例題
2けたの自然数と、その数の十の位の数と一の位の数を入れかえでできる数 との和が11の倍数になる ことを 説明しなさ い。
中2数学「式による説明②(連続する数)」【毎日配信】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中二~第十回 式による説明②~
例題
連続する3つの整数の和は、3の倍数になることを説明しなさい。
この動画を見る
中二~第十回 式による説明②~
例題
連続する3つの整数の和は、3の倍数になることを説明しなさい。
