【中学数学】2次方程式：数に関する問題② 差が3で、積が40になる2つの負の数を求めよ。 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中３数学 > ２次方程式 > 【中学数学】2次方程式：数に関する問題②　差が3で、積が40になる2つの負の数を求めよ。

【中学数学】2次方程式：数に関する問題②　差が3で、積が40になる2つの負の数を求めよ。

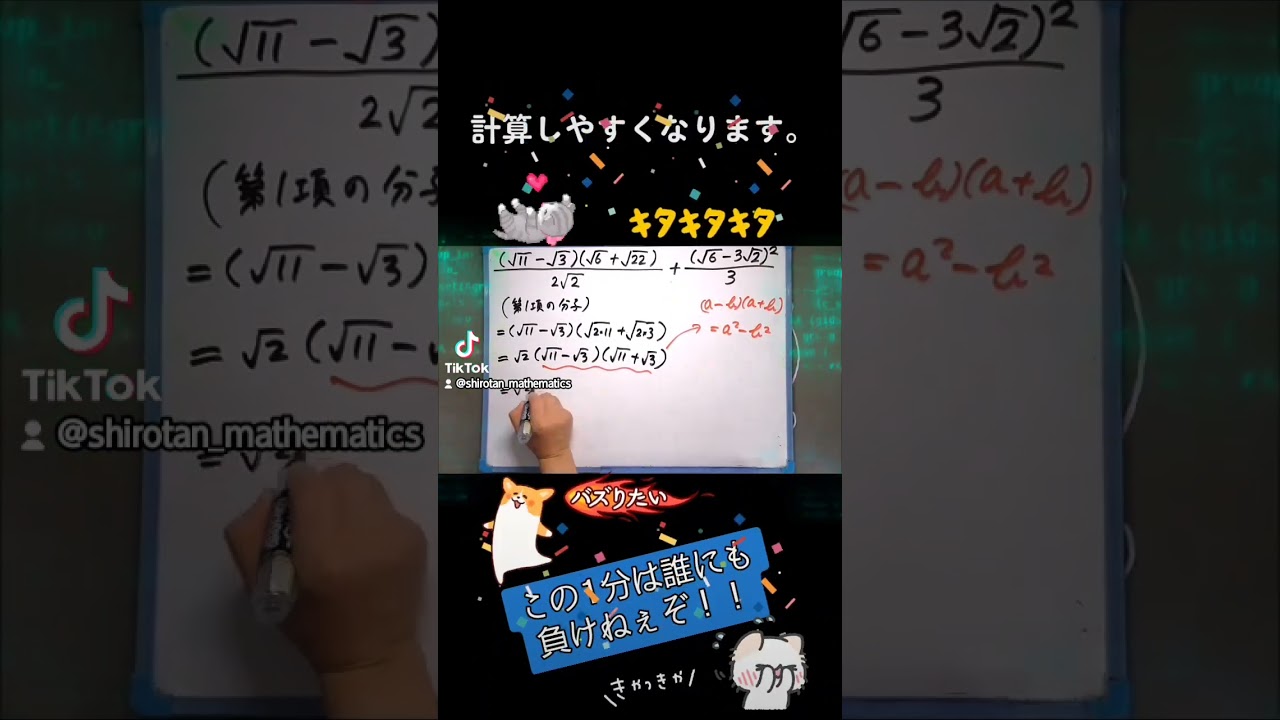
問題文全文(内容文)：
差が3で、積が40になる2つの負の数を求めよ。
チャプター：

0:00 オープニング
0:05 問題文
0:11 問題解説
2:57 名言

単元： #数学(中学生)#中３数学#２次方程式
指導講師： 理数個別チャンネル
問題文全文(内容文)：
差が3で、積が40になる2つの負の数を求めよ。
投稿日：2020.08.25

＜関連動画＞

この計算でもとに戻る理由は？

アイキャッチ画像
単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
「この計算でもとに戻る理由」について解説しています。
※問題文は動画内参照
この動画を見る　

二次方程式：東京都立八王子東高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題　東京都立八王子東高等学校

次の問いに答えよ。
2次方程式
$(x + 4)^2−6(x + 4) + 7 = 0 $
を解け。
この動画を見る　

【…で、実際の解き方は？】二次方程式：法政大学第二高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2次方程式$(2x+3)^2=(3x-8)^2$を解きなさい.

法政大第二高校過去問
この動画を見る　

三角形と内接円　東大寺学園

アイキャッチ画像
単元： #数学(中学生)#中３数学#相似な図形
指導講師： 数学を数楽に
問題文全文(内容文)：
$MD=?$
この動画を見る　

【数学】中3-62 三平方の定理②(練習編)

アイキャッチ画像
単元： #数学(中学生)#中３数学#三平方の定理
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
①2辺の長さが4cm、8cmの正方形の対角線の長さは？

②2つの対角線の長さが12cm、16cmのひし形の1辺の長さは？

③BDの長さは？
※図は動画内参照

④次の長さを③辺とすると㋐～㋒の中で直角三角形はどれ？
㋐5cm、8cm、6cm
㋑$2\sqrt{ 2 }cm、2\sqrt{ 3 }cm、2\sqrt{ 5 }cm$
㋒$2cm、2\sqrt{ 3 }cm、3cm$
この動画を見る　
PAGE TOP