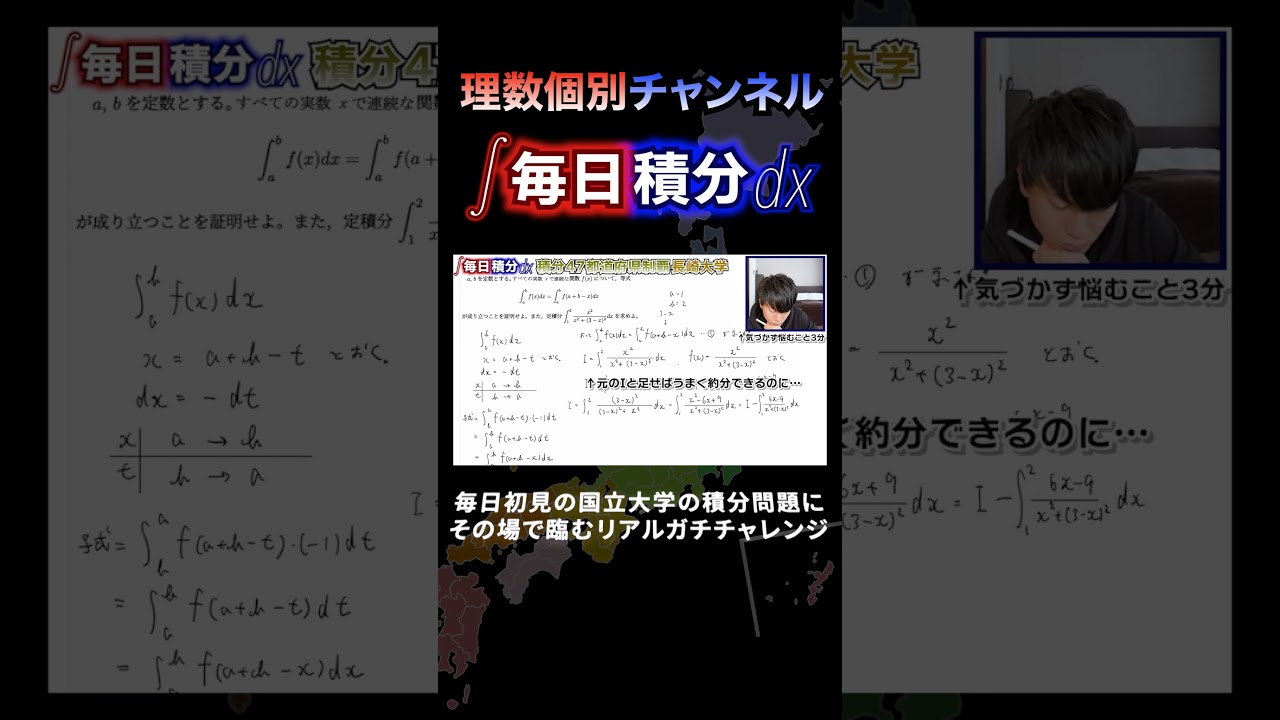
問題文全文(内容文):
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
投稿日:2020.01.16