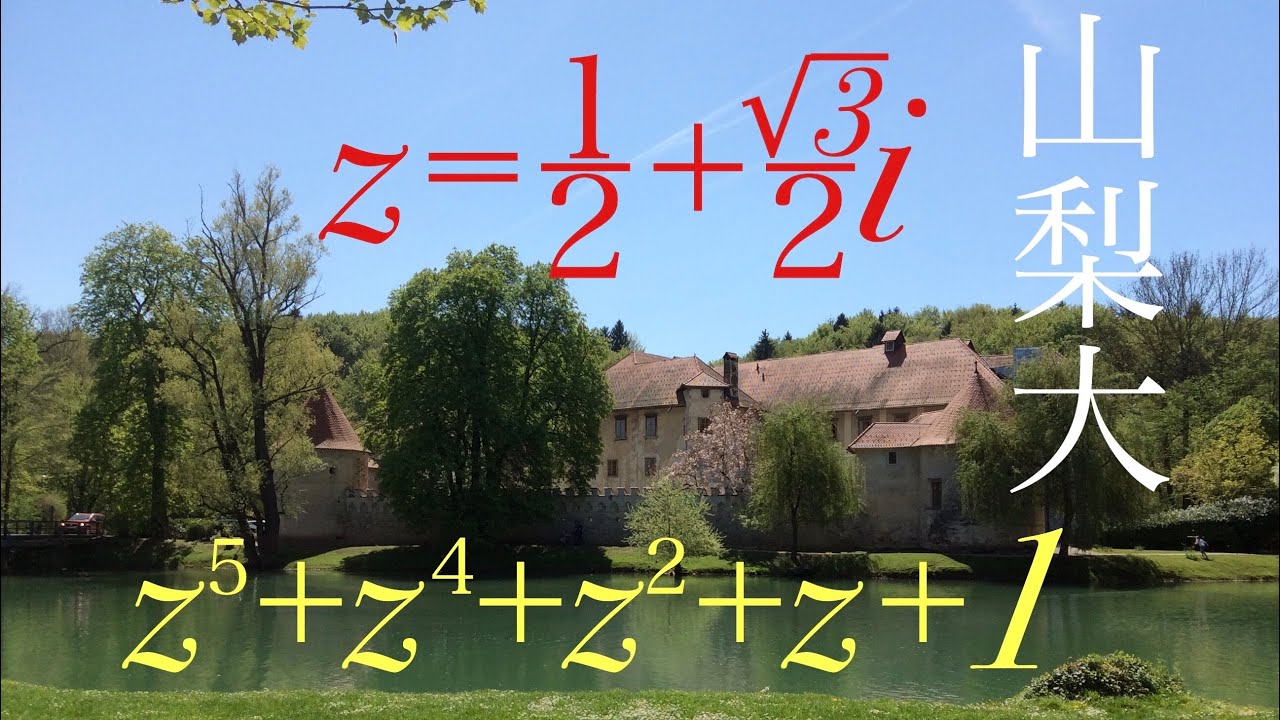複素数日本大 - 質問解決D.B.（データベース）

問題文全文(内容文)：
これを解け.
$z=\dfrac{\sqrt6+\sqrt2}{4}+\dfrac{\sqrt6-\sqrt2}{4}i$,$\displaystyle \sum_{n=1}^{23}z^n$

2000日大過去問

単元： #数Ⅱ#複素数と方程式#複素数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
これを解け.
$z=\dfrac{\sqrt6+\sqrt2}{4}+\dfrac{\sqrt6-\sqrt2}{4}i$,$\displaystyle \sum_{n=1}^{23}z^n$

2000日大過去問

投稿日：2020.05.28

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#防衛医科大学

指導講師：ますただ

問題文全文(内容文)：
$z^3=8$の虚数解の1つを$\alpha$とする。
$\alpha^4+6\alpha^3+8\alpha^2+8\alpha$の値を求めよ。

出典：2020年防衛医科大学　入試問題

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数C#茨城大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
近畿大学過去問題
$x^4-Px^2+P^2-P-2=0$が相異4実根をもつPの範囲

茨城大学過去問題
$x^3=i$を解け

この動画を見る　

単元： #数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C

指導講師：鈴木貫太郎

問題文全文(内容文)：
$x^2+i=0$を解け

出典：1971年神戸大学　過去問

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$\Large{\boxed{1}}$ (2)複素数$z$の方程式
$z^2$-3|$z$|+2=0
を考える。この方程式は$\boxed{\ \ イ\ \ }$個の解を持ち、このうち実数でないかの個数は$\boxed{\ \ ウ\ \ }$個である。

この動画を見る　

単元： #数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
$\boxed{7}$ $\vert Z \vert=1,Z^5=1$
$Z\leftarrow \in $を求めよ.

この動画を見る　