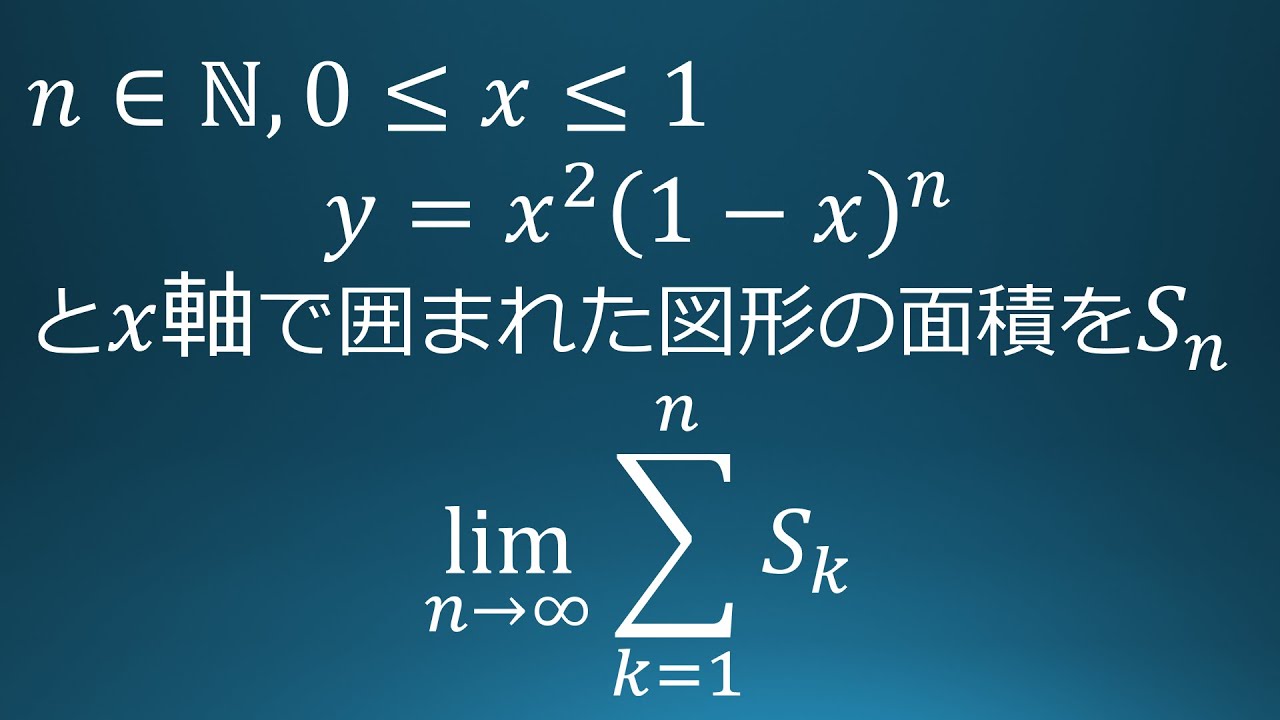問題文全文(内容文):
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
チャプター:
0:00 大問1(1)
2:38 大問1(2)
4:13 大問1(3)
6:03 大問2
14:25 大問3
20:56 大問4
29:38 エンディング
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
投稿日:2023.11.23