問題文全文(内容文)：
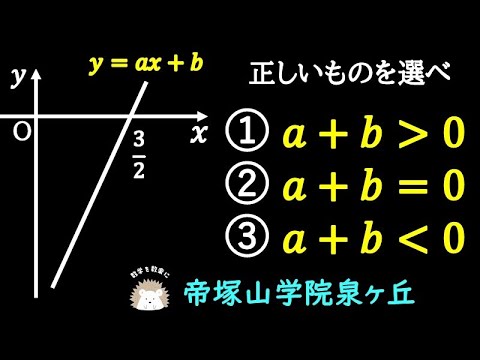
一次関数といえば、y=①＿＿＿＿

◎水槽に8cmの高さまで水が入っている。
この水槽に1分間に3cmの割合で水を入れる。
水を入れはじめてからx分後の底から水面までの高さをycmとするとき、下の表の空欄を埋めよう。
※表は動画内参照

⑦yをxの式で表すと？

◎長さ10cmのろうそくに火をつけると毎分0.5cmの割合で短くなる。
火をつけてからx分後のろうそくの長さをycmとする。
⑧yをxの式で表すと？
⑨6分後のろうそくの長さは？
⑩ろうそくの長さが3cmになるのは何分後？
⑪yの値の範囲は？
⑫xの値の範囲は？