問題文全文(内容文):
高校受験対策・関数44
Q
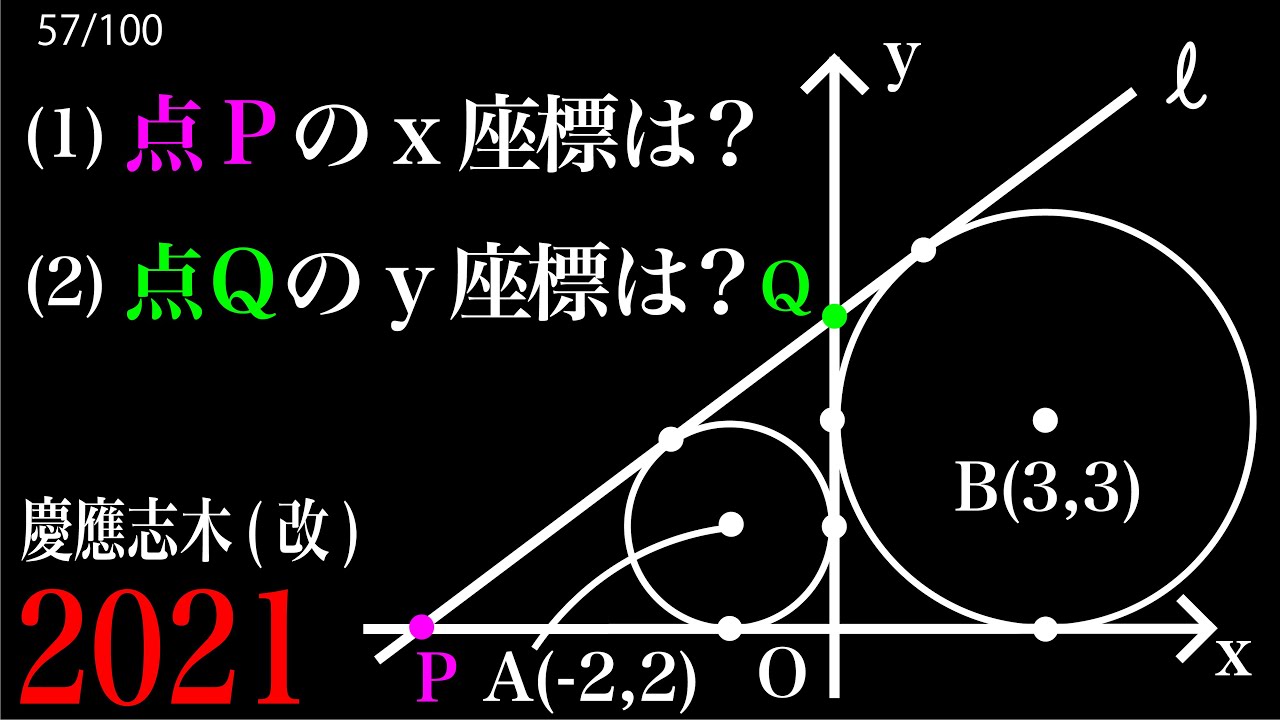
右の図で、点Oは原点であり、放物線①は関数$y=x^2$のグラフ で、直線②は関数$y=x-1$のグラフである。
点Aは直線②上の点で、その$x$座標は$-2$であり、点Pは放物線①上の点で、その$x$座標は正の数である。
点Pを通り$y$軸に平行な直線をひき、直線②との交点をQとする。
また、点Aを通り$x$軸に平行な直線をひき、直線PQとの 交点をRとする。
これについて、次の(1)、(2)の問いに答えよ。
(1)関数$y=x^2$で、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めよ。
(2)線分PQの長さと、線分QRの長さが等しになるとき、点Pの$x$座標はいくつか求めよ。
高校受験対策・関数44
Q
右の図で、点Oは原点であり、放物線①は関数$y=x^2$のグラフ で、直線②は関数$y=x-1$のグラフである。
点Aは直線②上の点で、その$x$座標は$-2$であり、点Pは放物線①上の点で、その$x$座標は正の数である。
点Pを通り$y$軸に平行な直線をひき、直線②との交点をQとする。
また、点Aを通り$x$軸に平行な直線をひき、直線PQとの 交点をRとする。
これについて、次の(1)、(2)の問いに答えよ。
(1)関数$y=x^2$で、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めよ。
(2)線分PQの長さと、線分QRの長さが等しになるとき、点Pの$x$座標はいくつか求めよ。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数44
Q
右の図で、点Oは原点であり、放物線①は関数$y=x^2$のグラフ で、直線②は関数$y=x-1$のグラフである。
点Aは直線②上の点で、その$x$座標は$-2$であり、点Pは放物線①上の点で、その$x$座標は正の数である。
点Pを通り$y$軸に平行な直線をひき、直線②との交点をQとする。
また、点Aを通り$x$軸に平行な直線をひき、直線PQとの 交点をRとする。
これについて、次の(1)、(2)の問いに答えよ。
(1)関数$y=x^2$で、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めよ。
(2)線分PQの長さと、線分QRの長さが等しになるとき、点Pの$x$座標はいくつか求めよ。
高校受験対策・関数44
Q
右の図で、点Oは原点であり、放物線①は関数$y=x^2$のグラフ で、直線②は関数$y=x-1$のグラフである。
点Aは直線②上の点で、その$x$座標は$-2$であり、点Pは放物線①上の点で、その$x$座標は正の数である。
点Pを通り$y$軸に平行な直線をひき、直線②との交点をQとする。
また、点Aを通り$x$軸に平行な直線をひき、直線PQとの 交点をRとする。
これについて、次の(1)、(2)の問いに答えよ。
(1)関数$y=x^2$で、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めよ。
(2)線分PQの長さと、線分QRの長さが等しになるとき、点Pの$x$座標はいくつか求めよ。
投稿日:2019.12.28