問題文全文(内容文):
高校受験対策・図形31
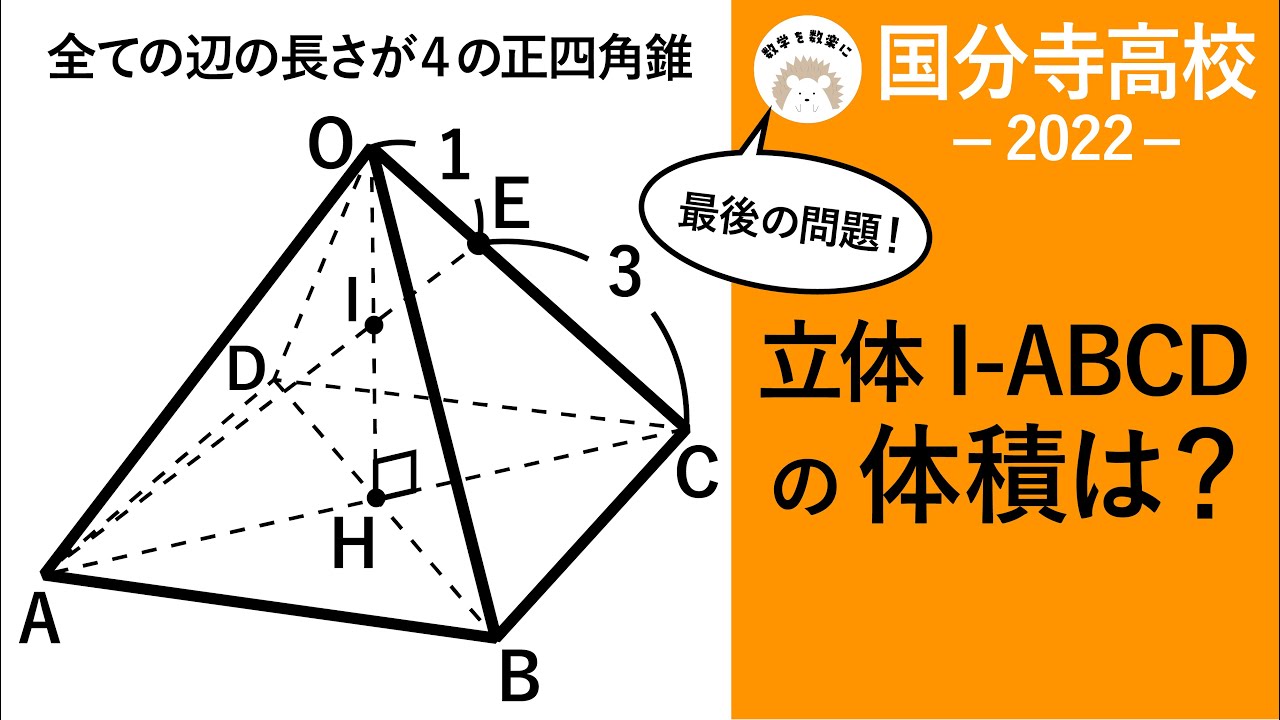
Q.
下の図のように、AB=6cm、 BC=8cm、CA=3cm、BE=12cmの三角柱ABC-DEFがある。
点Pは、点Bを出発して辺BE上を毎秒1cmの速さで動き、点で停止する。
点Qは、点Cを出 発して辺CF上を毎秒2cmの速さで動き、点Fで折り返して点Cに戻ったところで停止する。
2点P、Qが同時に出発し、出発してからの時間を$x$秒$(0 \leqq x \leqq 12)$とする。
このことについて、次の問いに答えなさい。
①$0 \leqq x \leqq 6$のとき、四角形PBCQの面積を$x$を使って表せ。
②$6 \leqq x \leqq 12$のとき、四角形PBCQの面積を$x$を使って表せ。
③線分PQが長方形BCFEの面積を2等分するときの$x$の値をすべて求めよ。
④三角DPQがDP=DQの二等辺三角形となるとき、線分PQの長さを求めよ。
高校受験対策・図形31
Q.
下の図のように、AB=6cm、 BC=8cm、CA=3cm、BE=12cmの三角柱ABC-DEFがある。
点Pは、点Bを出発して辺BE上を毎秒1cmの速さで動き、点で停止する。
点Qは、点Cを出 発して辺CF上を毎秒2cmの速さで動き、点Fで折り返して点Cに戻ったところで停止する。
2点P、Qが同時に出発し、出発してからの時間を$x$秒$(0 \leqq x \leqq 12)$とする。
このことについて、次の問いに答えなさい。
①$0 \leqq x \leqq 6$のとき、四角形PBCQの面積を$x$を使って表せ。
②$6 \leqq x \leqq 12$のとき、四角形PBCQの面積を$x$を使って表せ。
③線分PQが長方形BCFEの面積を2等分するときの$x$の値をすべて求めよ。
④三角DPQがDP=DQの二等辺三角形となるとき、線分PQの長さを求めよ。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形31
Q.
下の図のように、AB=6cm、 BC=8cm、CA=3cm、BE=12cmの三角柱ABC-DEFがある。
点Pは、点Bを出発して辺BE上を毎秒1cmの速さで動き、点で停止する。
点Qは、点Cを出 発して辺CF上を毎秒2cmの速さで動き、点Fで折り返して点Cに戻ったところで停止する。
2点P、Qが同時に出発し、出発してからの時間を$x$秒$(0 \leqq x \leqq 12)$とする。
このことについて、次の問いに答えなさい。
①$0 \leqq x \leqq 6$のとき、四角形PBCQの面積を$x$を使って表せ。
②$6 \leqq x \leqq 12$のとき、四角形PBCQの面積を$x$を使って表せ。
③線分PQが長方形BCFEの面積を2等分するときの$x$の値をすべて求めよ。
④三角DPQがDP=DQの二等辺三角形となるとき、線分PQの長さを求めよ。
高校受験対策・図形31
Q.
下の図のように、AB=6cm、 BC=8cm、CA=3cm、BE=12cmの三角柱ABC-DEFがある。
点Pは、点Bを出発して辺BE上を毎秒1cmの速さで動き、点で停止する。
点Qは、点Cを出 発して辺CF上を毎秒2cmの速さで動き、点Fで折り返して点Cに戻ったところで停止する。
2点P、Qが同時に出発し、出発してからの時間を$x$秒$(0 \leqq x \leqq 12)$とする。
このことについて、次の問いに答えなさい。
①$0 \leqq x \leqq 6$のとき、四角形PBCQの面積を$x$を使って表せ。
②$6 \leqq x \leqq 12$のとき、四角形PBCQの面積を$x$を使って表せ。
③線分PQが長方形BCFEの面積を2等分するときの$x$の値をすべて求めよ。
④三角DPQがDP=DQの二等辺三角形となるとき、線分PQの長さを求めよ。
投稿日:2019.12.27