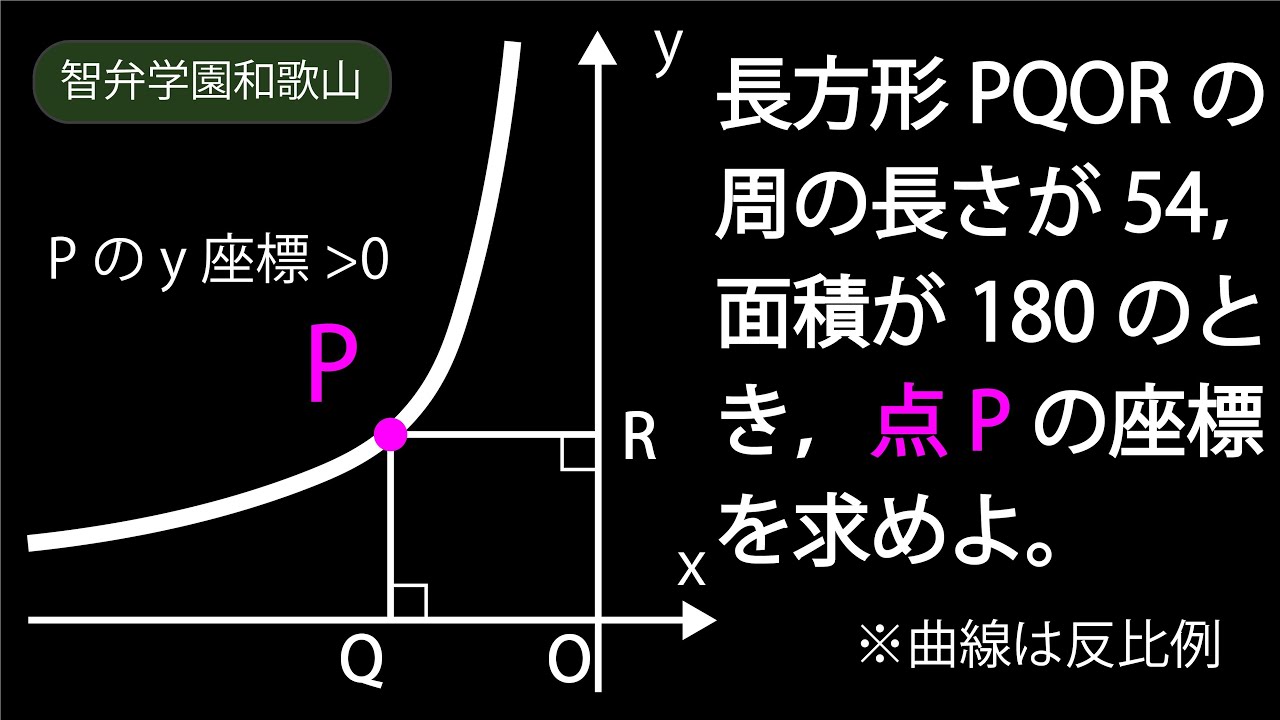
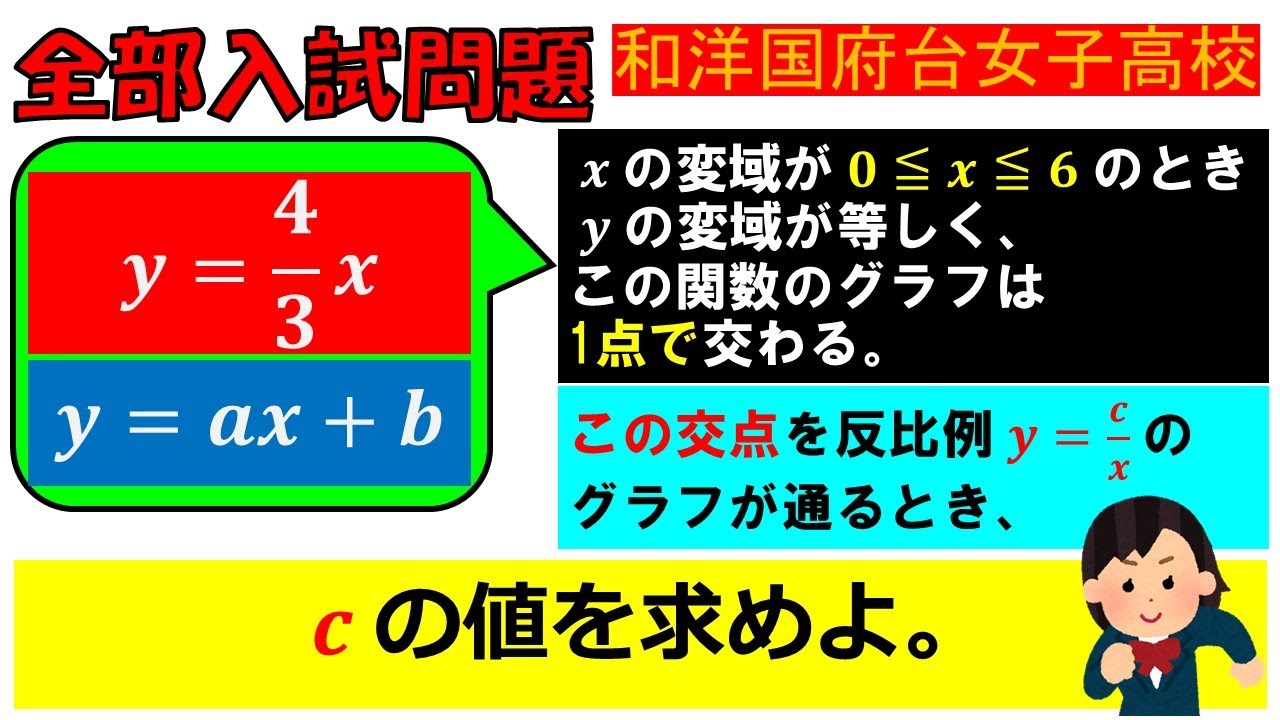
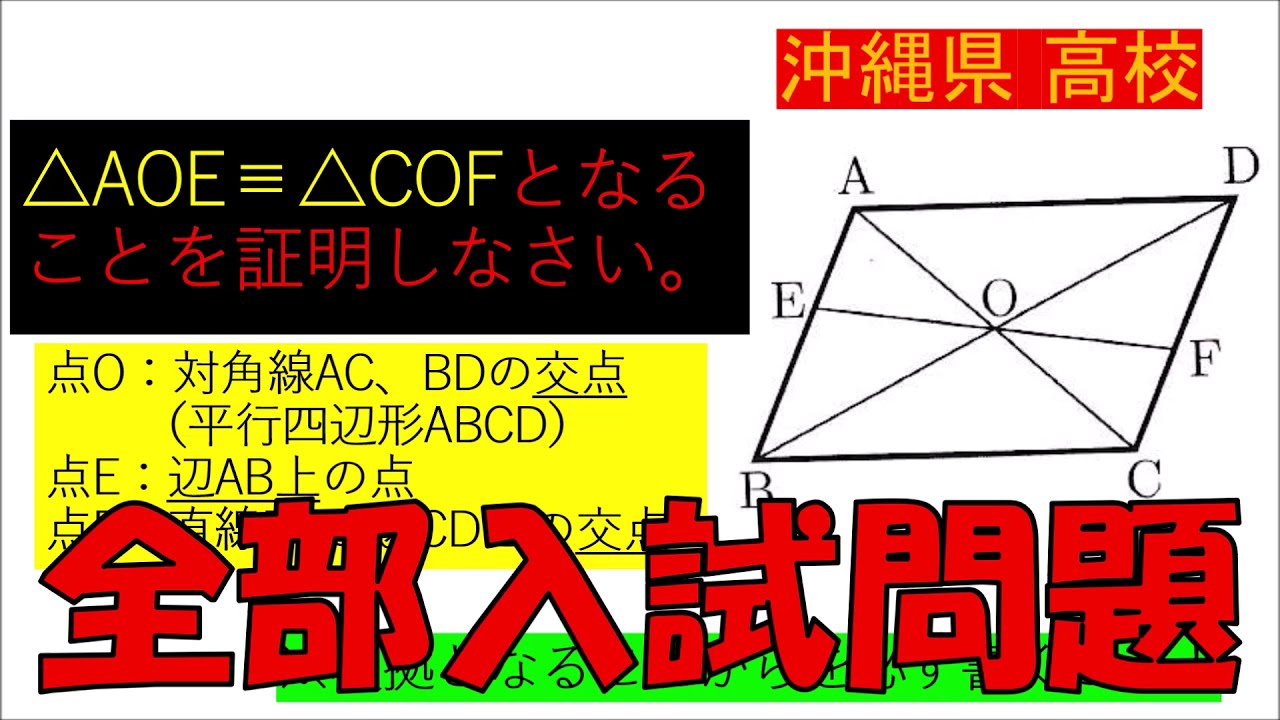
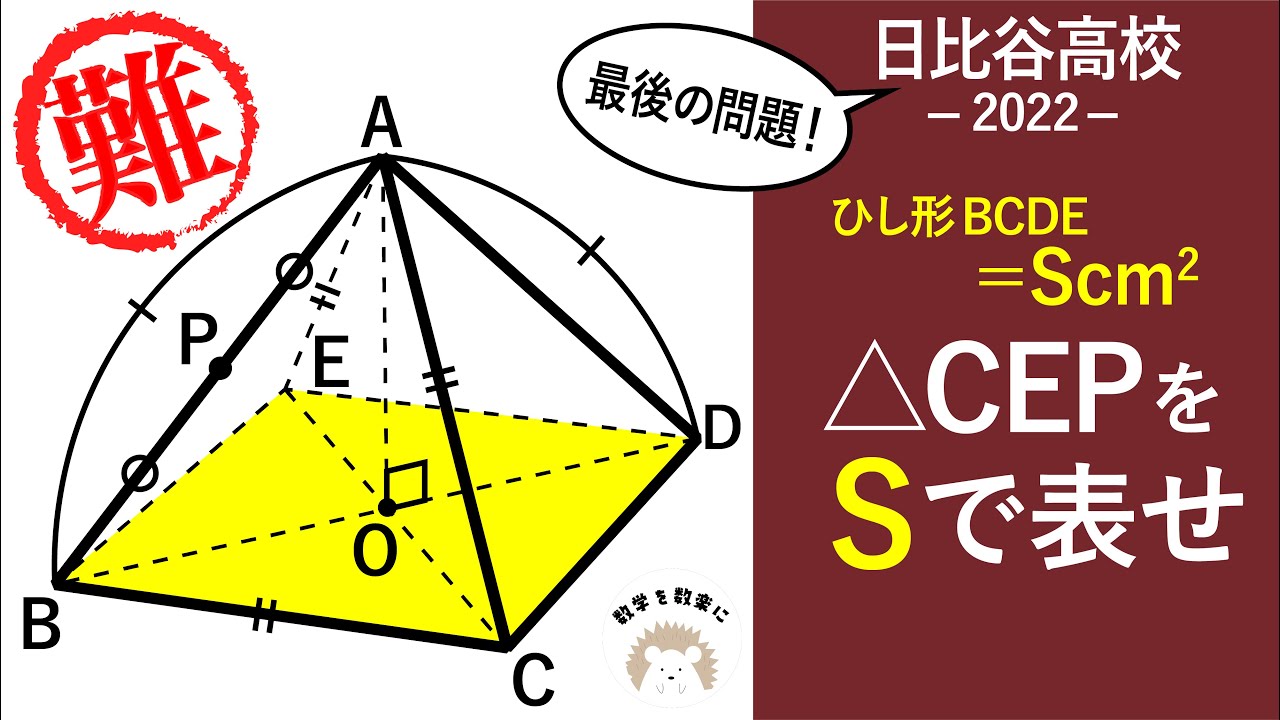
問題文全文(内容文):
高校受験対策・死守39
①$-7+5$
➁$(-3) \times4-(-6)×4$
③$\frac{2}{3}\div -\frac{8}{3}+\frac{1}{2}$
④$4(-x+3y)-5(x+2y)$
⑤$\frac{14}{\sqrt{7}}+\sqrt{3}\times\sqrt{21}$
⑥$x^2+5x-36$を因数分解しなさい。
⑦2次方程式$3x^2+3x-1=0$を解きなさい。
⑧$x$についての方程式$3x-4=x-2a$の解が$5$であるとき、$a$の値を求めなさい。
⑨$n$を自然数とするとき、$4 \lt \sqrt{n}\lt 10$をみたす$n$の値は何個あるか求めなさい。
➉下の図のように$△ABC$がある。
このとき、$△ABC$を点$o$を中心として点対称移動させた図形をかきなさい。
高校受験対策・死守39
①$-7+5$
➁$(-3) \times4-(-6)×4$
③$\frac{2}{3}\div -\frac{8}{3}+\frac{1}{2}$
④$4(-x+3y)-5(x+2y)$
⑤$\frac{14}{\sqrt{7}}+\sqrt{3}\times\sqrt{21}$
⑥$x^2+5x-36$を因数分解しなさい。
⑦2次方程式$3x^2+3x-1=0$を解きなさい。
⑧$x$についての方程式$3x-4=x-2a$の解が$5$であるとき、$a$の値を求めなさい。
⑨$n$を自然数とするとき、$4 \lt \sqrt{n}\lt 10$をみたす$n$の値は何個あるか求めなさい。
➉下の図のように$△ABC$がある。
このとき、$△ABC$を点$o$を中心として点対称移動させた図形をかきなさい。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守39
①$-7+5$
➁$(-3) \times4-(-6)×4$
③$\frac{2}{3}\div -\frac{8}{3}+\frac{1}{2}$
④$4(-x+3y)-5(x+2y)$
⑤$\frac{14}{\sqrt{7}}+\sqrt{3}\times\sqrt{21}$
⑥$x^2+5x-36$を因数分解しなさい。
⑦2次方程式$3x^2+3x-1=0$を解きなさい。
⑧$x$についての方程式$3x-4=x-2a$の解が$5$であるとき、$a$の値を求めなさい。
⑨$n$を自然数とするとき、$4 \lt \sqrt{n}\lt 10$をみたす$n$の値は何個あるか求めなさい。
➉下の図のように$△ABC$がある。
このとき、$△ABC$を点$o$を中心として点対称移動させた図形をかきなさい。
高校受験対策・死守39
①$-7+5$
➁$(-3) \times4-(-6)×4$
③$\frac{2}{3}\div -\frac{8}{3}+\frac{1}{2}$
④$4(-x+3y)-5(x+2y)$
⑤$\frac{14}{\sqrt{7}}+\sqrt{3}\times\sqrt{21}$
⑥$x^2+5x-36$を因数分解しなさい。
⑦2次方程式$3x^2+3x-1=0$を解きなさい。
⑧$x$についての方程式$3x-4=x-2a$の解が$5$であるとき、$a$の値を求めなさい。
⑨$n$を自然数とするとき、$4 \lt \sqrt{n}\lt 10$をみたす$n$の値は何個あるか求めなさい。
➉下の図のように$△ABC$がある。
このとき、$△ABC$を点$o$を中心として点対称移動させた図形をかきなさい。
投稿日:2019.10.16