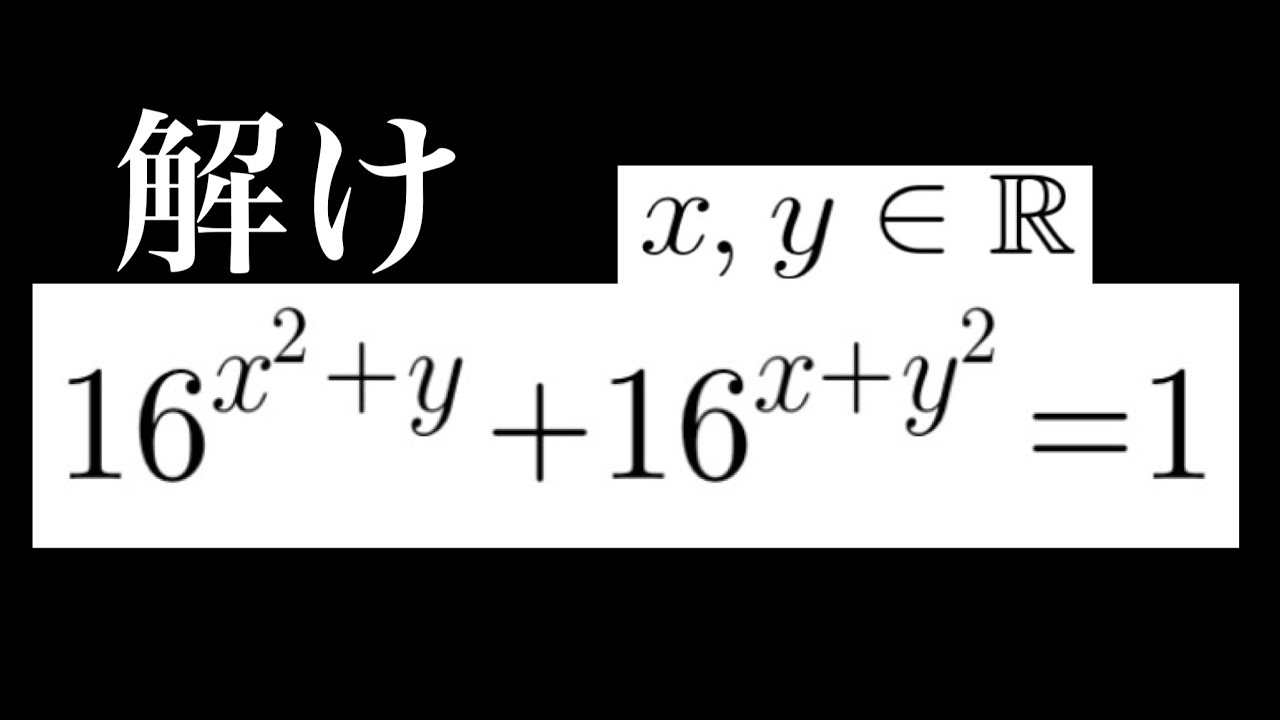問題文全文(内容文):
◎次の不等式を解こう。
$2^{x}-32 \gt 0$
$(\displaystyle \frac{1}{3})^{x-1} \leqq \displaystyle \frac{1}{27}$
$(\displaystyle \frac{1}{4})^{x} \leqq 2^{x+2}$
$16^{x}-3・4^{x}-4 \leqq 0$
$(\displaystyle \frac{1}{3})^{2x-1}+5・(\displaystyle \frac{1}{3})^{x}-2 \lt 0$
◎次の不等式を解こう。
$2^{x}-32 \gt 0$
$(\displaystyle \frac{1}{3})^{x-1} \leqq \displaystyle \frac{1}{27}$
$(\displaystyle \frac{1}{4})^{x} \leqq 2^{x+2}$
$16^{x}-3・4^{x}-4 \leqq 0$
$(\displaystyle \frac{1}{3})^{2x-1}+5・(\displaystyle \frac{1}{3})^{x}-2 \lt 0$
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の不等式を解こう。
$2^{x}-32 \gt 0$
$(\displaystyle \frac{1}{3})^{x-1} \leqq \displaystyle \frac{1}{27}$
$(\displaystyle \frac{1}{4})^{x} \leqq 2^{x+2}$
$16^{x}-3・4^{x}-4 \leqq 0$
$(\displaystyle \frac{1}{3})^{2x-1}+5・(\displaystyle \frac{1}{3})^{x}-2 \lt 0$
◎次の不等式を解こう。
$2^{x}-32 \gt 0$
$(\displaystyle \frac{1}{3})^{x-1} \leqq \displaystyle \frac{1}{27}$
$(\displaystyle \frac{1}{4})^{x} \leqq 2^{x+2}$
$16^{x}-3・4^{x}-4 \leqq 0$
$(\displaystyle \frac{1}{3})^{2x-1}+5・(\displaystyle \frac{1}{3})^{x}-2 \lt 0$
投稿日:2015.09.16