福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第4問〜正四面体の切り口の面積の最小値 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 大学入試過去問(数学) > 学校別大学入試過去問解説(数学) > 東京慈恵会医科大学 > 福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第4問〜正四面体の切り口の面積の最小値

福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第4問〜正四面体の切り口の面積の最小値

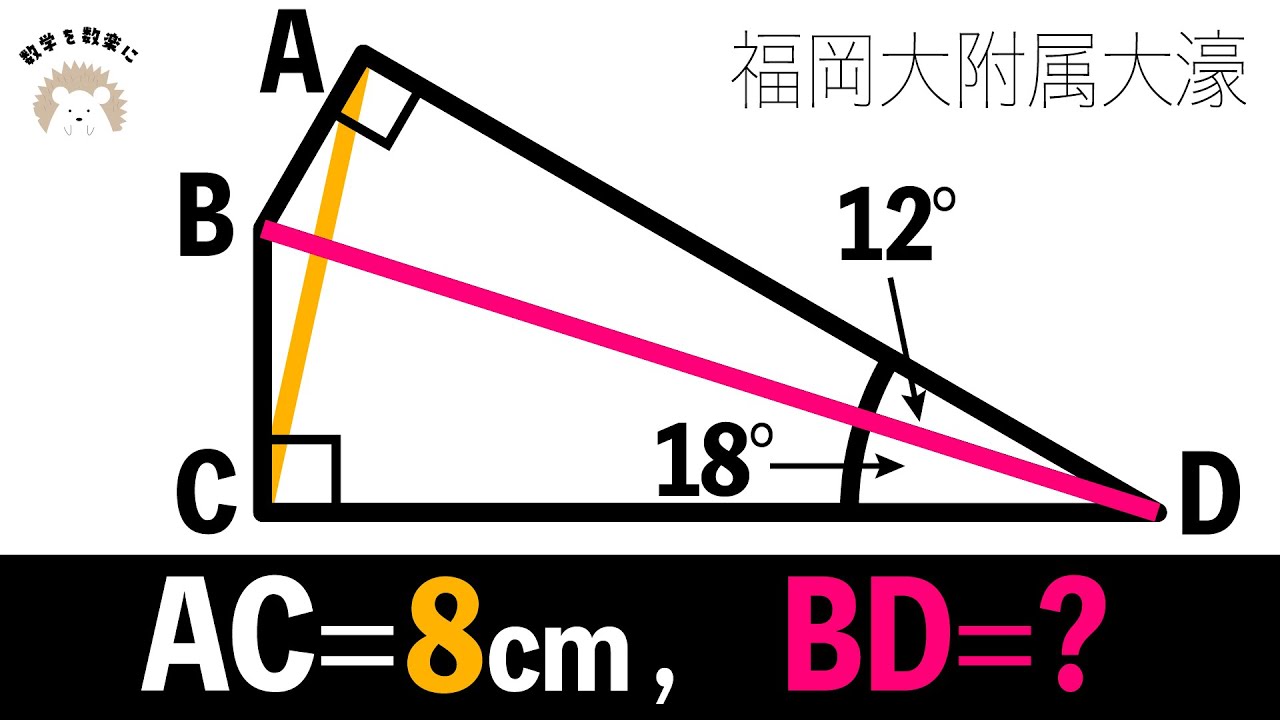
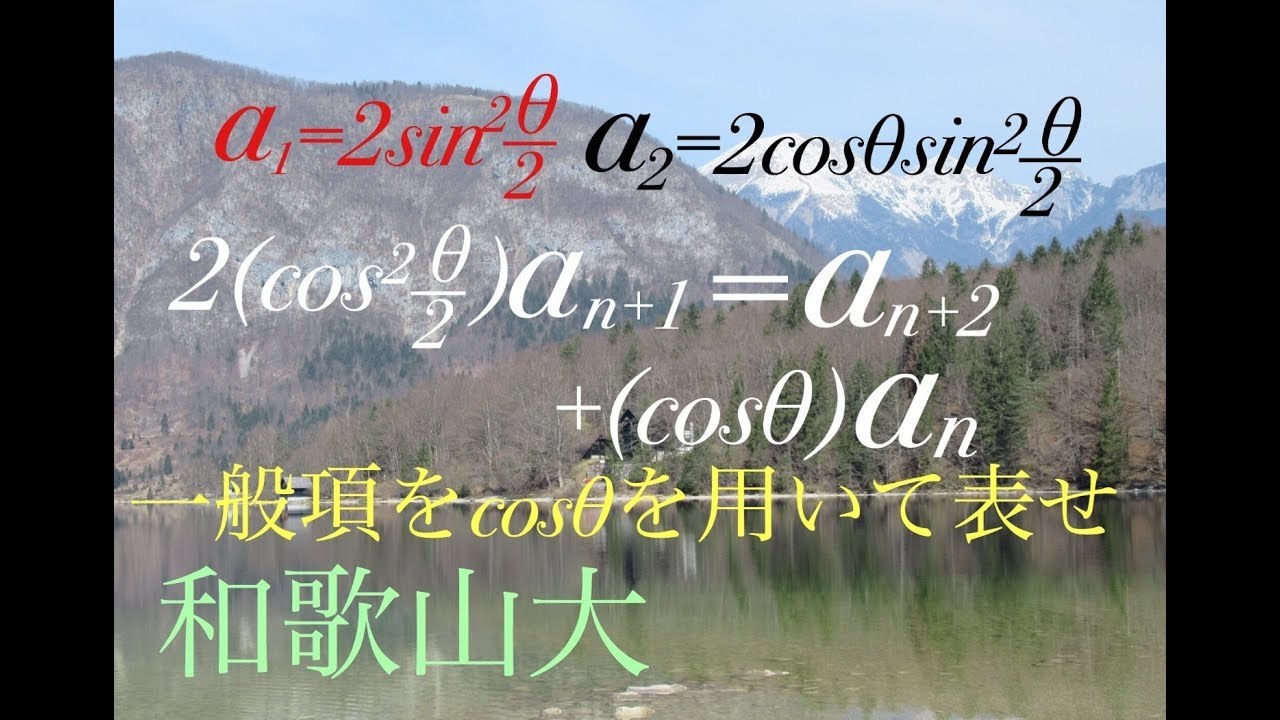問題文全文(内容文)：
oを原点とするxyz 空間内に、xy平面上の放物線y=x²をy軸のまわりに回転してできる曲面Sと、正四面体OABCがあり、条件「3頂点A, B, CはS上にある」をみたしている。このとき、次の問いに答えよ。
(1)正四面体 OABCの1辺の長さを求めよ。
(2)正四面体 OABCが条件をみたしながら動くとき、xy平面による正四面体OABCの切り口の面積の最小値を求めよ。
単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師： 福田次郎
問題文全文(内容文)：
oを原点とするxyz 空間内に、xy平面上の放物線y=x²をy軸のまわりに回転してできる曲面Sと、正四面体OABCがあり、条件「3頂点A, B, CはS上にある」をみたしている。このとき、次の問いに答えよ。
(1)正四面体 OABCの1辺の長さを求めよ。
(2)正四面体 OABCが条件をみたしながら動くとき、xy平面による正四面体OABCの切り口の面積の最小値を求めよ。
投稿日：2025.01.21

＜関連動画＞

どう解くか？だ。

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
方程式を解け
$0.2(0.1x -0.8) = \frac{4x+7}{50}$

法政大学
この動画を見る　

電気通信大学2014年　#定積分　#Shorts

アイキャッチ画像
単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師： ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$

出典：2014年電気通信大学
この動画を見る　

早稲田　学習院　高校数学 Mathematics Japanese university entrance exam

アイキャッチ画像
単元： #数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
学習院大学過去問題
$x^3+y^3=3xy$ (x,y実数)
x+yのとりうる範囲

早稲田大学過去問題
$a_1$~$a_n$整数
$x^n+a_1x^{n-1}+a_2x^{n-2}+\cdots+a_{n-1}x+a_n=0$
整数係数のn次方程式、解が有理数ならその解は整数である。
この動画を見る　

数学「大学入試良問集」【12−2 微分と直方体の体積】を宇宙一わかりやすく

アイキャッチ画像
単元： #大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#朝日大学
指導講師： ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
縦$x$、横$y$、高さ$z$の和が12、表面積が90であるような直方体を考える。
（1）$y+z$および$yz$を$x$の式で表せ。
（2）このような直方体が存在するための$x$の範囲を求めよ。
（3）このような直方体のうち体積が最大であるものを求めよ。
この動画を見る　

数学「大学入試良問集」【19−2 三角関数の面積の二等分】を宇宙一わかりやすく

アイキャッチ画像
単元： #大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#京都府立医科大学
指導講師： ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
次の不等式が定める図形を$D$とする。
$0 \leqq x \leqq \displaystyle \frac{\pi}{2},0 \leqq y \leqq \sin2x$
（1）
曲線$y=a\ \sin\ x$と$y=\sin2x$が$0 \lt x \lt \displaystyle \frac{\pi}{2}$で交わるような定数$a$の範囲を求めよ。

（2）
曲線$y=a\ \sin\ x$が図形$D$を面積の等しい2つの部分に分けるような定数$a$を求めよ。
この動画を見る　
Back to top