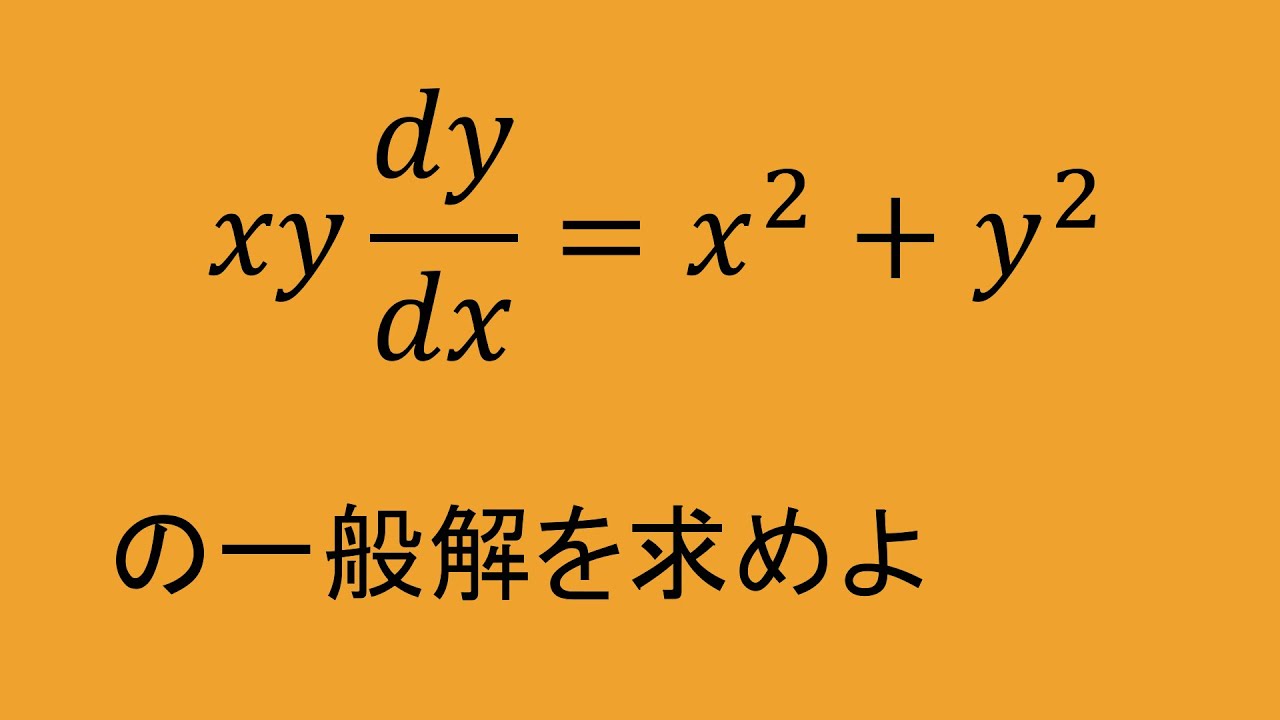#1微分方程式練習問題（高専数学数検1級） - 質問解決D.B.（データベース）

問題文全文(内容文)：
$ x\dfrac{dy}{dx}=y(\log y-\log x+1)$
の一般解を求めよ.

単元： #数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$ x\dfrac{dy}{dx}=y(\log y-\log x+1)$
の一般解を求めよ.

投稿日：2021.05.14

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級

指導講師：ますただ

問題文全文(内容文)：
$\sin(\sin^{-1}(-\displaystyle \frac{5}{13})+\cos^{-1}(\displaystyle \frac{4}{5}))$の値を求めよ。

出典：数検1級1次　過去問

この動画を見る　

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。

この動画を見る　

指導講師：ますただ

問題文全文(内容文)：
$x\dfrac{dy}{dx}+y=y^2\log x$の
一般解を求めよ.

この動画を見る　

単元： #数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#数学検定#数学検定1級#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
方程式
$x^8-8x^6+20x^4-17x^2+4=0$を解け。

この動画を見る　

単元： #数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\sqrt[ 3 ]{ \sqrt{ 5 }+2 }$の値を求めよ

この動画を見る　