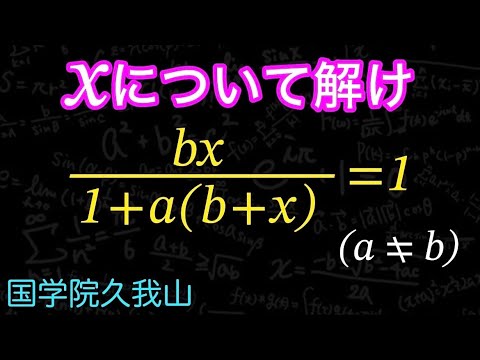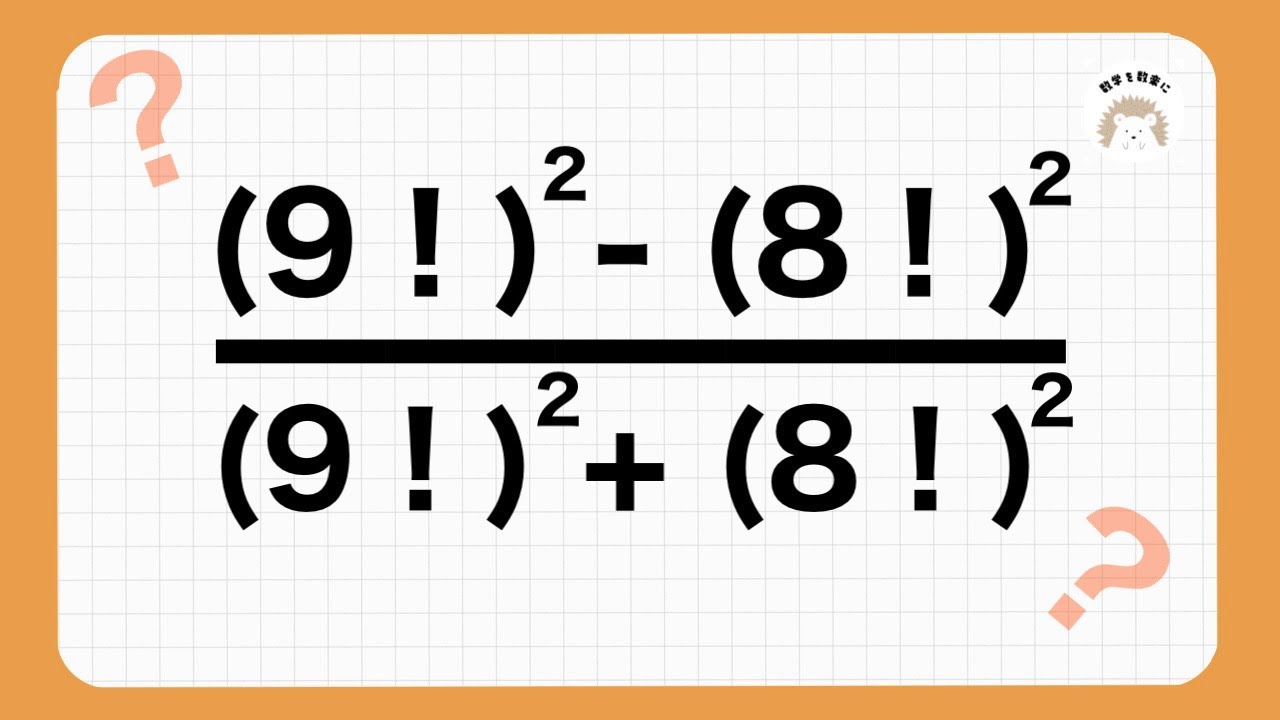問題文全文(内容文):
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
投稿日:2016.06.23