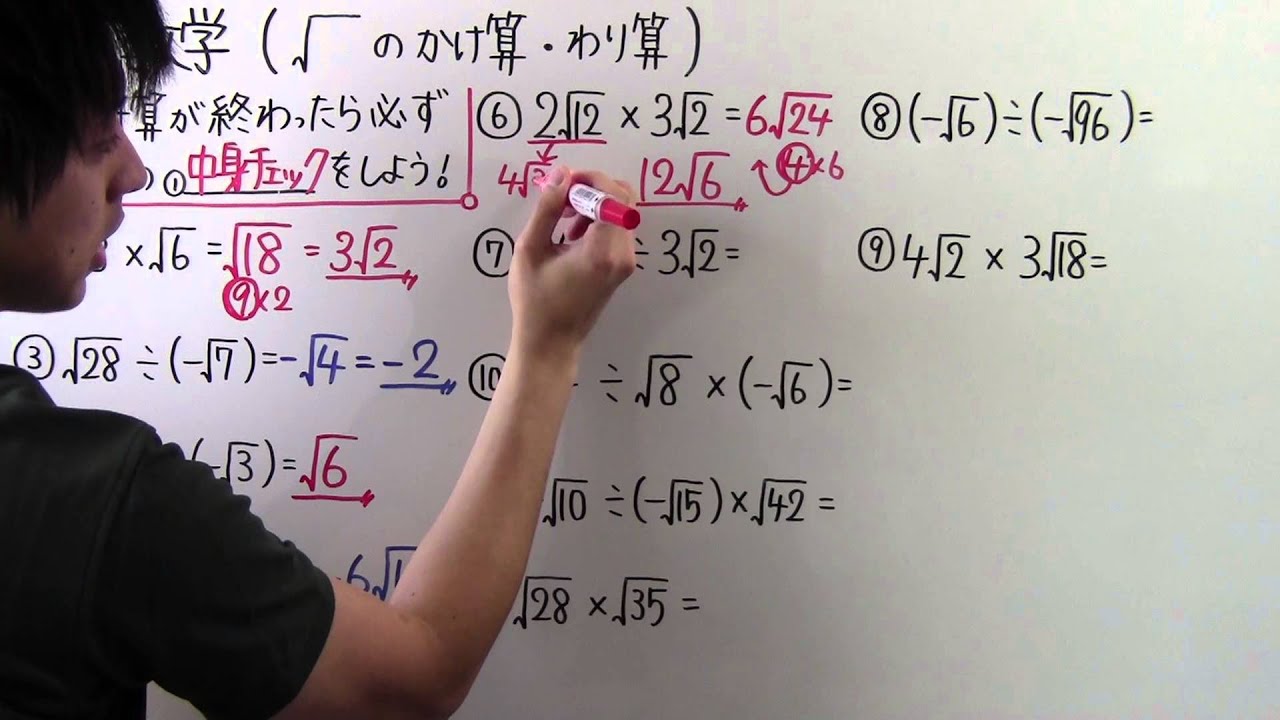【数学】中高一貫校問題集2幾何98：円：円周角の定理：弧の長さの和 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中３数学 > 円 > 【数学】中高一貫校問題集2幾何98：円：円周角の定理：弧の長さの和

【数学】中高一貫校問題集2幾何98：円：円周角の定理：弧の長さの和

問題文全文(内容文)：
半径4cmの円Oの内部に点Pをとり、図のようにPで直交する円Oの弦AB、CDを引く。このとき、弧ACの長さと弧BDの長さの和を求めなさい。
チャプター：

0:00 オープニング
0:05 問題文
0:22 解説
1:43 エンディング

単元： #数学(中学生)#中３数学#円
教材： #TK数学#TK数学問題集2(幾何編)#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
半径4cmの円Oの内部に点Pをとり、図のようにPで直交する円Oの弦AB、CDを引く。このとき、弧ACの長さと弧BDの長さの和を求めなさい。
投稿日：2023.10.04

＜関連動画＞

三平方の定理を使わずに解くこともできます

アイキャッチ画像
単元： #数学(中学生)#中２数学#中３数学#三平方の定理#三角形と四角形
指導講師： 数学を数楽に
問題文全文(内容文)：
x=?
＊図は動画内参照
この動画を見る　

【総合力が試される5分間！】二次方程式：和洋国府台女子高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題　和洋国府台女子高等学校

【二次方程式】
$x^2-4x-3=0$
この方程式の解のうち、 大きい方の解の
整数部分:a
小数部分:b
　↓
$ab+b^2$
の値を求めよ。
この動画を見る　

2001を素因数分解せよ　土佐高校

アイキャッチ画像
単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
$\sqrt{676} = ?$
2001を素因数分解せよ。

2011土佐高等学校
この動画を見る　

【数学】中高一貫校問題集2幾何140：円：方べきの定理：√5の作図

アイキャッチ画像
単元： #数学(中学生)#中３数学#円
教材： #TK数学#TK数学問題集2(幾何編)#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
長さ1の線分ABから、長さ√5の線分を次の手順で作図できる。
①線分ABのBを超える延長線上に、BC=5となる点Cをとる。
②線分ACを直径とする円Oをかく。
③Bを通り、直線ABに垂直な直線を引き、点Oとの交点をD、Eとする。
(1)長さが√5の線分を次のうちからすべて答えなさい。
AD,AE,AO,BD,BO,CD,CE,CO,DO,EO
(2)(1)で答えた線分の長さが√5であることを証明しなさい。
この動画を見る　

「2次方程式」と理解して100倍素早く解く裏ワザ～全国入試問題解法 #shorts #数学 #入試問題 #動体視力

アイキャッチ画像
単元： #数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
二次方程式$ ax^2+2x+b=0 $の解が$ x=2 $のただ1つである.
定数$ a,b $の値をそれぞれ求めなさい.

立命館高校過去問
この動画を見る　
PAGE TOP