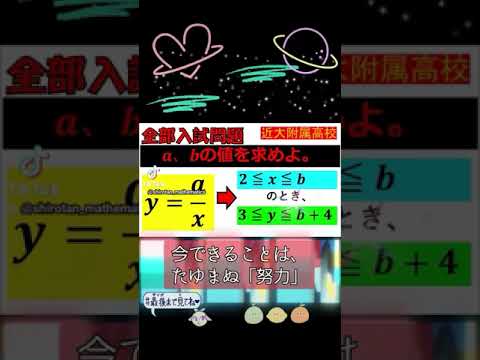
問題文全文(内容文):
A:半径4㎝の球、B:Aの二等分、C:Aの四等分の表面積の比を最も簡単な整数の比で表しなさい。
A:半径4㎝の球、B:Aの二等分、C:Aの四等分の表面積の比を最も簡単な整数の比で表しなさい。
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
A:半径4㎝の球、B:Aの二等分、C:Aの四等分の表面積の比を最も簡単な整数の比で表しなさい。
A:半径4㎝の球、B:Aの二等分、C:Aの四等分の表面積の比を最も簡単な整数の比で表しなさい。
投稿日:2025.05.06