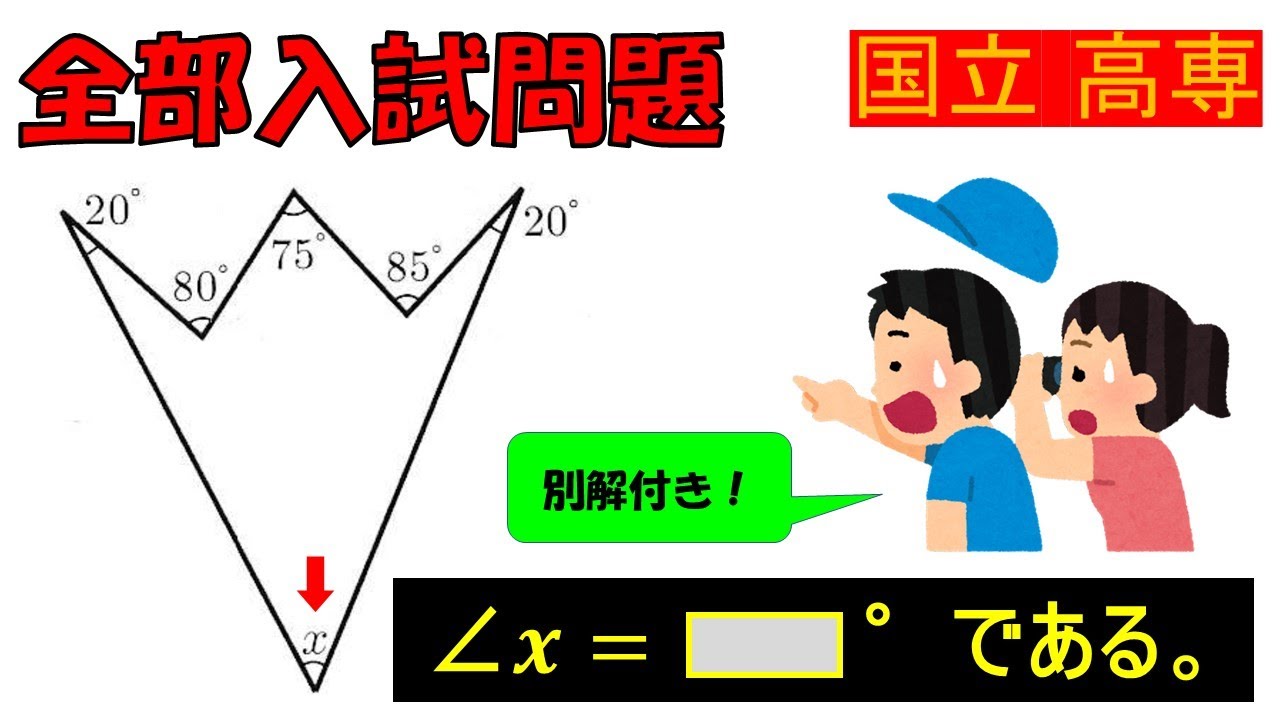
問題文全文(内容文):
興南高等学校の入試から、不等式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
興南高等学校の入試から、不等式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
興南高等学校の入試から、不等式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
興南高等学校の入試から、不等式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
投稿日:2025.04.25