【受験算数】平面図形：折り返した図形【慶應中等部2021】

問題文全文(内容文)：
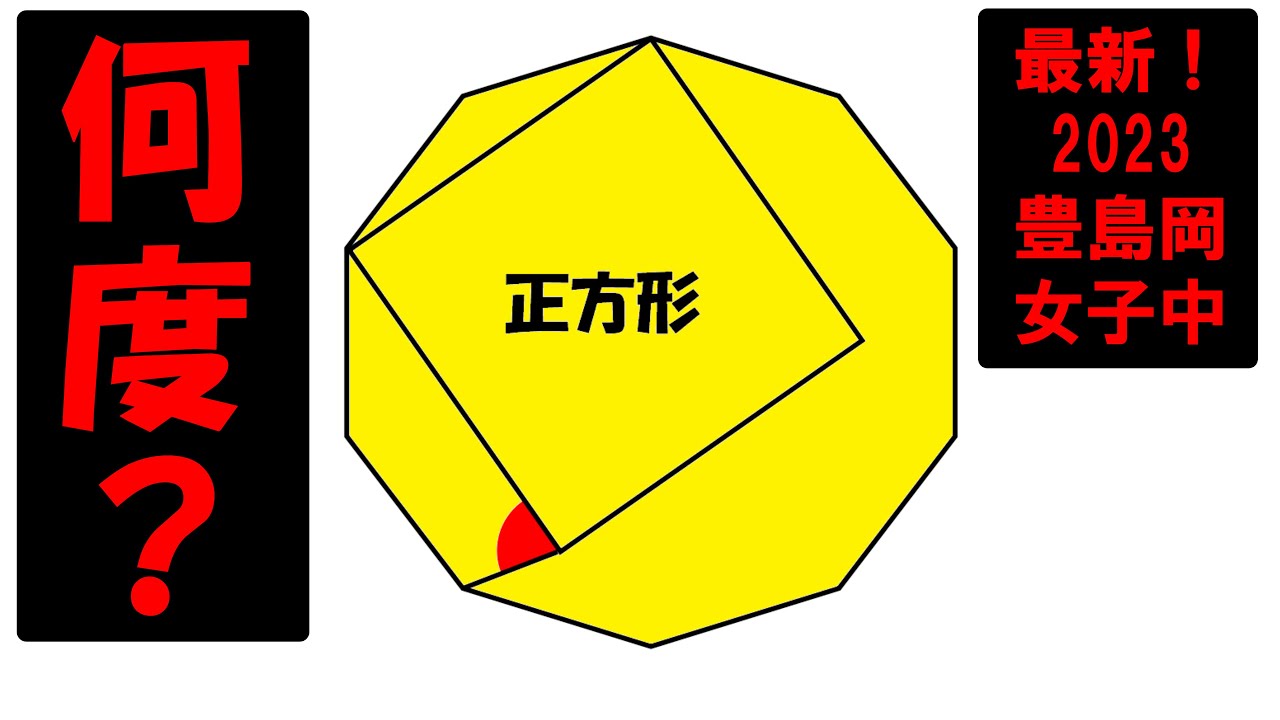
図のようなおうぎの形を、点Oが円周上の点に重なるように直線ABで折り返しました。このとき、角アの大きさを求めなさい。

チャプター：

0:00 オープニング
0:05 解説
1:50 エンディング

単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部

指導講師：理数個別チャンネル

問題文全文(内容文)：
図のようなおうぎの形を、点Oが円周上の点に重なるように直線ABで折り返しました。このとき、角アの大きさを求めなさい。

投稿日：2025.01.15

単元： #数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
a:b=?
＊図は動画内参照

西大和学園高等学校

この動画を見る　

単元： #算数(中学受験)#平面図形#角度と面積

指導講師：算数・数学ちゃんねる

問題文全文(内容文)：
正方形の折り紙を写真のように折った場合、
赤い矢印の部分は何度になるか求めよ。

※写真は動画内参照

この動画を見る　

単元： #算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{3}{13} + \frac{8}{19} + \frac{3}{22} + \frac{1}{33} + \frac{3}{38} +\frac{4}{39}$

吉祥寺女子中学校

この動画を見る　

単元： #算数(中学受験)#計算と数の性質#いろいろな計算

指導講師：算数・数学ちゃんねる

問題文全文(内容文)：
小学校のまとめ、中学受験の基礎（キソ）　文字と式7/8
・$□ \times 4+9=37$
・$□ \times 5+4=49$
・$x \times 11+10=131$

□/$x $の部分を求めよ。

この動画を見る　

単元： #算数(中学受験)#平面図形#相似と相似を利用した問題

指導講師：重吉

問題文全文(内容文)：
三角形$IHF$の面積は?

2024年昭和学院秀英中過去問

この動画を見る　