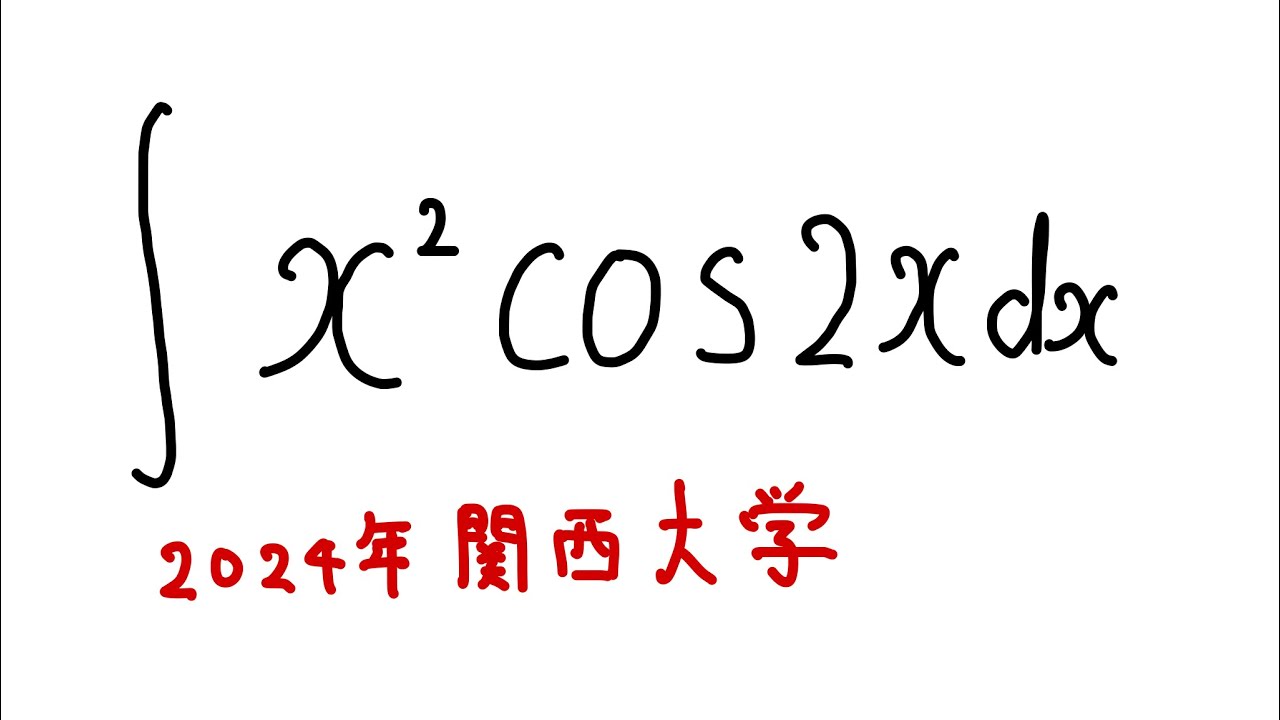問題文全文(内容文)：
曲面$x^2+y^2=1$ $(z \geqq 0)$と平面z=2x、xy平面で囲まれた体積Vを求めよ。
曲面$x^2+y^2=1$ $(z \geqq 0)$と平面z=2x、xy平面で囲まれた体積Vを求めよ。
単元：
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/single.php on line 102
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/single.php on line 103
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/single.php on line 102
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/single.php on line 103
指導講師：
ますただ
問題文全文(内容文)：
曲面$x^2+y^2=1$ $(z \geqq 0)$と平面z=2x、xy平面で囲まれた体積Vを求めよ。
曲面$x^2+y^2=1$ $(z \geqq 0)$と平面z=2x、xy平面で囲まれた体積Vを求めよ。
投稿日：2020.11.02