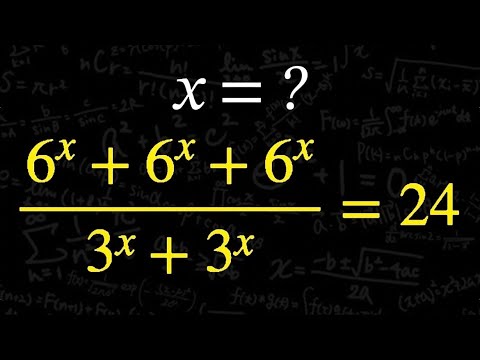問題文全文(内容文):
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
問題文全文(内容文):
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
投稿日:2022.07.15