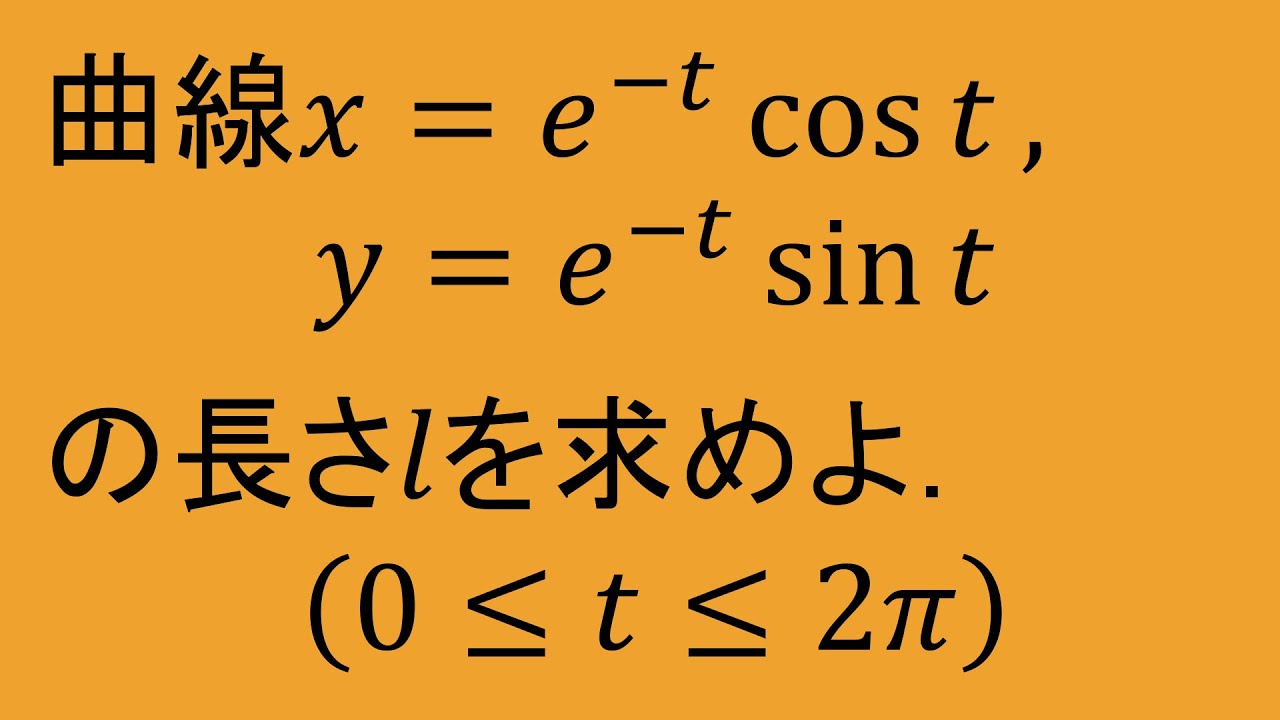福田のおもしろ数学152〜2つの図形の面積を同時に2等分する直線が存在する証明

問題文全文(内容文)：
次の2つの図形(※動画参照)の面積を同時に2等分する直線が存在することを証明せよ。

単元： #平面上の曲線#媒介変数表示と極座標#数C

指導講師：福田次郎

問題文全文(内容文)：
次の2つの図形(※動画参照)の面積を同時に2等分する直線が存在することを証明せよ。

投稿日：2024.05.31

単元： #平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C

教材： #4S数学#4S数学ⅢのB問題解説#中高教材#極限

指導講師：理数個別チャンネル

問題文全文(内容文)：
楕円 $\dfrac{x^2}{9}+\dfrac{y^2}{16}=1$ に内接し、
辺が座標軸に平行な長方形のうち、
面積が最大となる長方形の 2 辺の
長さおよび面積を、
媒介変数表示を利用して求めよ。

この動画を見る　

単元： #平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C

教材： #サクシード#サクシード数学Ⅲ#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
2直線
$r(\sqrt3\cos\theta+\sin\theta)=4$
$r(\sqrt3\cos\theta-\sin\theta)=2$
の交点の極座標を求めよ。またこの2直線のなす鋭角も求めよ。
（出典　数研出版サクシード数学Ⅲ）

この動画を見る　

単元： #数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C

指導講師：ますただ

問題文全文(内容文)：
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.

この動画を見る　

単元： #大学入試過去問(数学)#平面上の曲線#2次曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#京都大学#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
極方程式
$r=1+\cos\theta$
$(0 \leqq \theta \leqq \pi)$で表される曲線の長さ$l$を求めよ。

出典：2009年京都大学　入試問題

この動画を見る　

単元： #数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C

指導講師：ますただ

問題文全文(内容文)：
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.

この動画を見る　