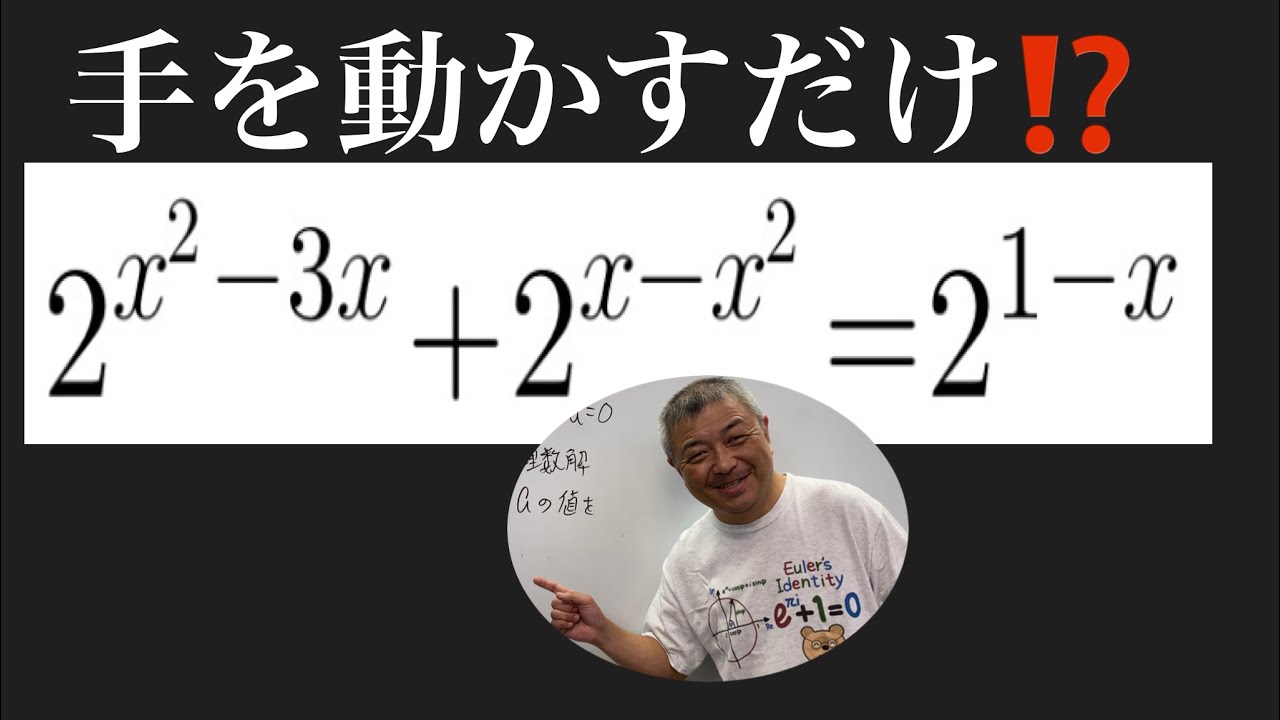福田のおもしろ数学354〜指数方程式

問題文全文(内容文)：
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。

投稿日：2024.12.21

単元： #数Ⅱ#指数関数と対数関数#微分法と積分法#指数関数#微分とその応用#微分法#数学(高校生)#数Ⅲ

指導講師：鈴木貫太郎

問題文全文(内容文)：
$e^π$と$π^e$どっちがでかい？

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
指数のフシギ〜お小遣いの悪魔の交渉術！？

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$(\frac{1}{9})^{0.3} \div (\frac{1}{27})^{0.2}$

この動画を見る　

単元： #大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数Ⅲ

指導講師：鈴木貫太郎

問題文全文(内容文)：
'89山形大学過去問題
$f(x)=x^4-6a^2x^2+5a^4$ (a＞0)
(a,0)における接線l。
f(x)とlとで囲まれる面積

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ 12^{a+b}=18^{2a-b}$とするとき,
$3^{\frac{a}{b}}$はいくつか?

この動画を見る　