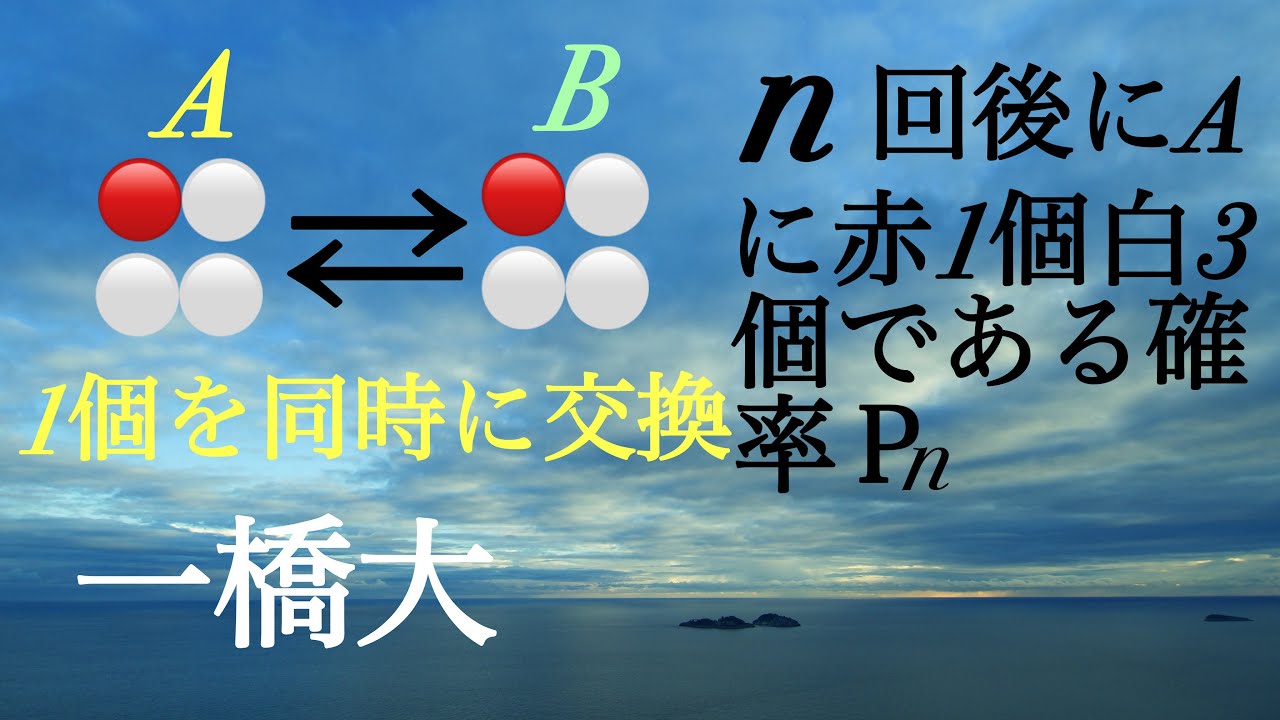
問題文全文(内容文):
①5種類の数字1,2,3,4,5を並べて3桁の整数をつくるとなん通りできる?
②5種類の数字1,2,3,4,5を重複を許して並べて3桁の整数をつくるとなん通りできる?
③4人が1回じゃんけんするとき、手の出し方は何通りある?
①5種類の数字1,2,3,4,5を並べて3桁の整数をつくるとなん通りできる?
②5種類の数字1,2,3,4,5を重複を許して並べて3桁の整数をつくるとなん通りできる?
③4人が1回じゃんけんするとき、手の出し方は何通りある?
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①5種類の数字1,2,3,4,5を並べて3桁の整数をつくるとなん通りできる?
②5種類の数字1,2,3,4,5を重複を許して並べて3桁の整数をつくるとなん通りできる?
③4人が1回じゃんけんするとき、手の出し方は何通りある?
①5種類の数字1,2,3,4,5を並べて3桁の整数をつくるとなん通りできる?
②5種類の数字1,2,3,4,5を重複を許して並べて3桁の整数をつくるとなん通りできる?
③4人が1回じゃんけんするとき、手の出し方は何通りある?
投稿日:2014.05.08