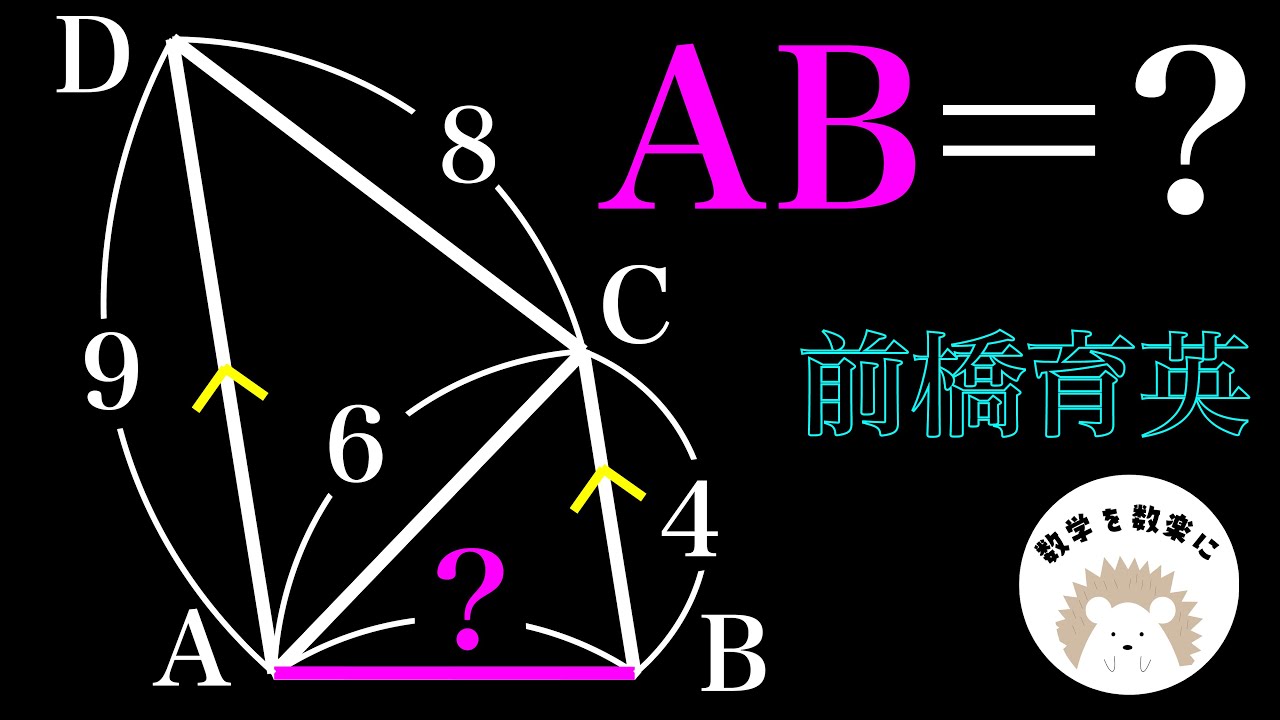問題文全文(内容文):
高校受験対策・死守41
①$5 \div\frac{1}{2} \times (-8)$を計算しなさい。
②$(\sqrt{7}-1)^2$を計算しなさい。
③$a=3$、$b=-4$のとき、 $(-ab)^3 \div ab^2$の値を求めなさい。
④2次方程式で$x^2=6x$を解きなさい。
⑤次の連立方程式を解きなさい。
$-x+2y=8$
$3x-y=6$
⑥4枚の硬貨を同時に投げたとき、表と裏が2枚ずつ出る確率を求めなさい。
⑦底面の半径が3cm、高さが4cmである円柱の表面積を求めなさい。
ただし円周率は$\pi$とする。
⑧右の図の円$o$において、$\angle x$の大きさを求めなさい。
⑨左の表はとある市における、7月の日ごとの最高気温を 度数分布表にまとめたものである。
次のア~エのうち、この表から読み取れることとして正しいものをすべて選び、記号で答えなさい。
ア 最高気温が37.0℃の日は5日あった。
イ 最高気温が40.0℃以上の日は1日もなかった
ウ 28,0℃以上 30.0℃未満の階級の相対度数は1である。
エ 中央値が含まれるのは34.0℃以上36.0℃未満の階級である。
高校受験対策・死守41
①$5 \div\frac{1}{2} \times (-8)$を計算しなさい。
②$(\sqrt{7}-1)^2$を計算しなさい。
③$a=3$、$b=-4$のとき、 $(-ab)^3 \div ab^2$の値を求めなさい。
④2次方程式で$x^2=6x$を解きなさい。
⑤次の連立方程式を解きなさい。
$-x+2y=8$
$3x-y=6$
⑥4枚の硬貨を同時に投げたとき、表と裏が2枚ずつ出る確率を求めなさい。
⑦底面の半径が3cm、高さが4cmである円柱の表面積を求めなさい。
ただし円周率は$\pi$とする。
⑧右の図の円$o$において、$\angle x$の大きさを求めなさい。
⑨左の表はとある市における、7月の日ごとの最高気温を 度数分布表にまとめたものである。
次のア~エのうち、この表から読み取れることとして正しいものをすべて選び、記号で答えなさい。
ア 最高気温が37.0℃の日は5日あった。
イ 最高気温が40.0℃以上の日は1日もなかった
ウ 28,0℃以上 30.0℃未満の階級の相対度数は1である。
エ 中央値が含まれるのは34.0℃以上36.0℃未満の階級である。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守41
①$5 \div\frac{1}{2} \times (-8)$を計算しなさい。
②$(\sqrt{7}-1)^2$を計算しなさい。
③$a=3$、$b=-4$のとき、 $(-ab)^3 \div ab^2$の値を求めなさい。
④2次方程式で$x^2=6x$を解きなさい。
⑤次の連立方程式を解きなさい。
$-x+2y=8$
$3x-y=6$
⑥4枚の硬貨を同時に投げたとき、表と裏が2枚ずつ出る確率を求めなさい。
⑦底面の半径が3cm、高さが4cmである円柱の表面積を求めなさい。
ただし円周率は$\pi$とする。
⑧右の図の円$o$において、$\angle x$の大きさを求めなさい。
⑨左の表はとある市における、7月の日ごとの最高気温を 度数分布表にまとめたものである。
次のア~エのうち、この表から読み取れることとして正しいものをすべて選び、記号で答えなさい。
ア 最高気温が37.0℃の日は5日あった。
イ 最高気温が40.0℃以上の日は1日もなかった
ウ 28,0℃以上 30.0℃未満の階級の相対度数は1である。
エ 中央値が含まれるのは34.0℃以上36.0℃未満の階級である。
高校受験対策・死守41
①$5 \div\frac{1}{2} \times (-8)$を計算しなさい。
②$(\sqrt{7}-1)^2$を計算しなさい。
③$a=3$、$b=-4$のとき、 $(-ab)^3 \div ab^2$の値を求めなさい。
④2次方程式で$x^2=6x$を解きなさい。
⑤次の連立方程式を解きなさい。
$-x+2y=8$
$3x-y=6$
⑥4枚の硬貨を同時に投げたとき、表と裏が2枚ずつ出る確率を求めなさい。
⑦底面の半径が3cm、高さが4cmである円柱の表面積を求めなさい。
ただし円周率は$\pi$とする。
⑧右の図の円$o$において、$\angle x$の大きさを求めなさい。
⑨左の表はとある市における、7月の日ごとの最高気温を 度数分布表にまとめたものである。
次のア~エのうち、この表から読み取れることとして正しいものをすべて選び、記号で答えなさい。
ア 最高気温が37.0℃の日は5日あった。
イ 最高気温が40.0℃以上の日は1日もなかった
ウ 28,0℃以上 30.0℃未満の階級の相対度数は1である。
エ 中央値が含まれるのは34.0℃以上36.0℃未満の階級である。
投稿日:2019.11.03