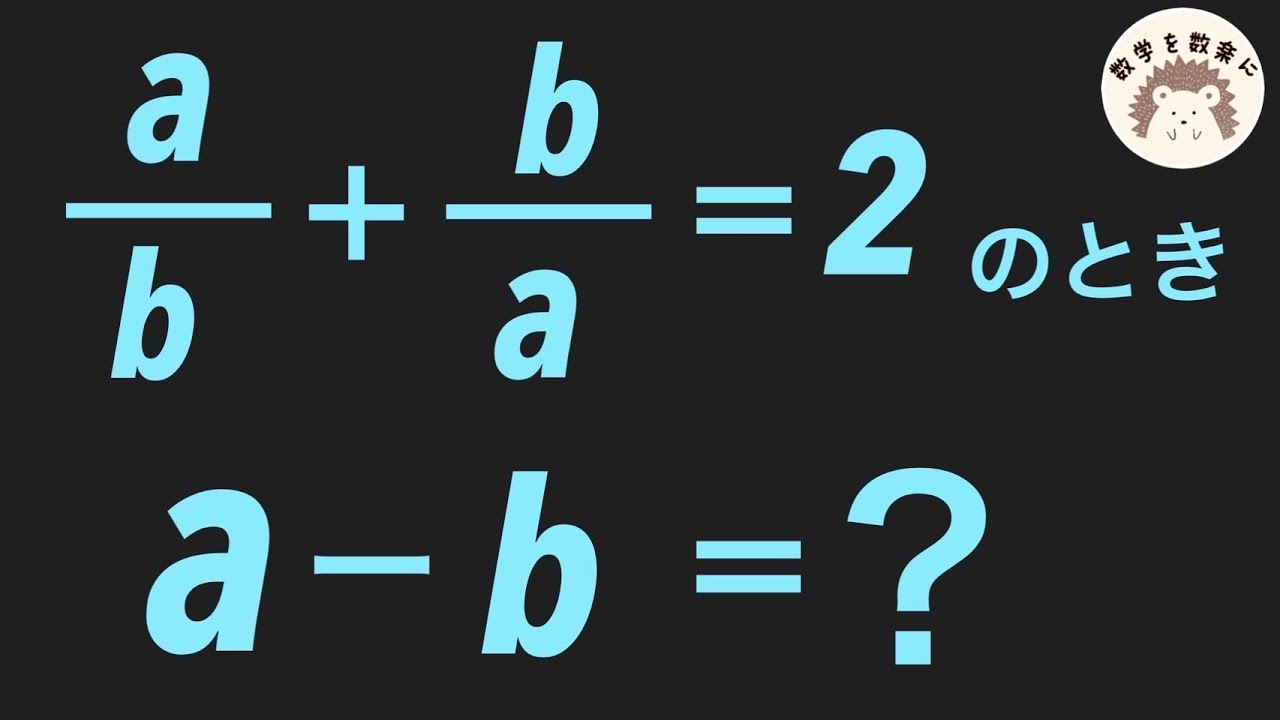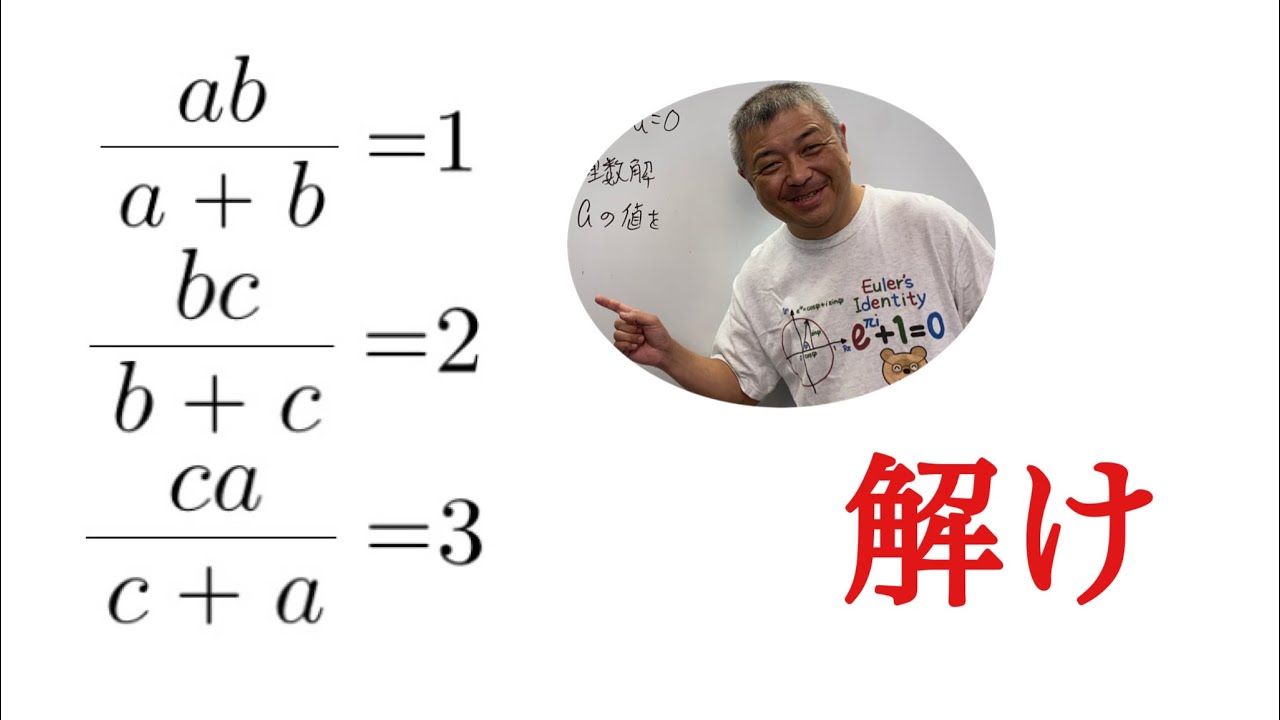問題文全文(内容文):
【ポイント】
三角形の合同条件は3種類!!
①____がそれぞれ等しいとき
②____________がそれぞれ等しいとき
③____________がそれぞれ等しいとき
④右の三角形から合同なものを選び、記号を使って表そう!
(合同条件はポイントの番号から選ぶ)
※図は動画内参照
【ポイント】
三角形の合同条件は3種類!!
①____がそれぞれ等しいとき
②____________がそれぞれ等しいとき
③____________がそれぞれ等しいとき
④右の三角形から合同なものを選び、記号を使って表そう!
(合同条件はポイントの番号から選ぶ)
※図は動画内参照
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【ポイント】
三角形の合同条件は3種類!!
①____がそれぞれ等しいとき
②____________がそれぞれ等しいとき
③____________がそれぞれ等しいとき
④右の三角形から合同なものを選び、記号を使って表そう!
(合同条件はポイントの番号から選ぶ)
※図は動画内参照
【ポイント】
三角形の合同条件は3種類!!
①____がそれぞれ等しいとき
②____________がそれぞれ等しいとき
③____________がそれぞれ等しいとき
④右の三角形から合同なものを選び、記号を使って表そう!
(合同条件はポイントの番号から選ぶ)
※図は動画内参照
投稿日:2013.11.02