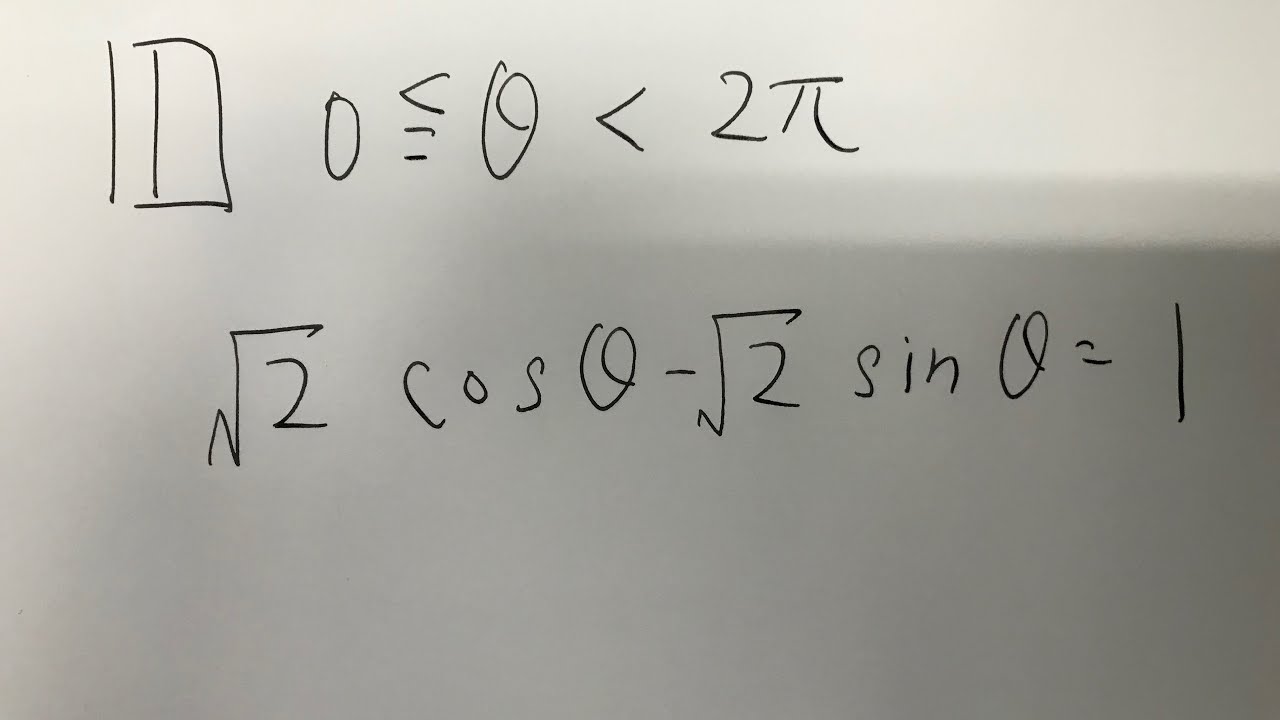問題文全文(内容文):
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
*$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
*$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
*$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
*$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
投稿日:2021.01.24