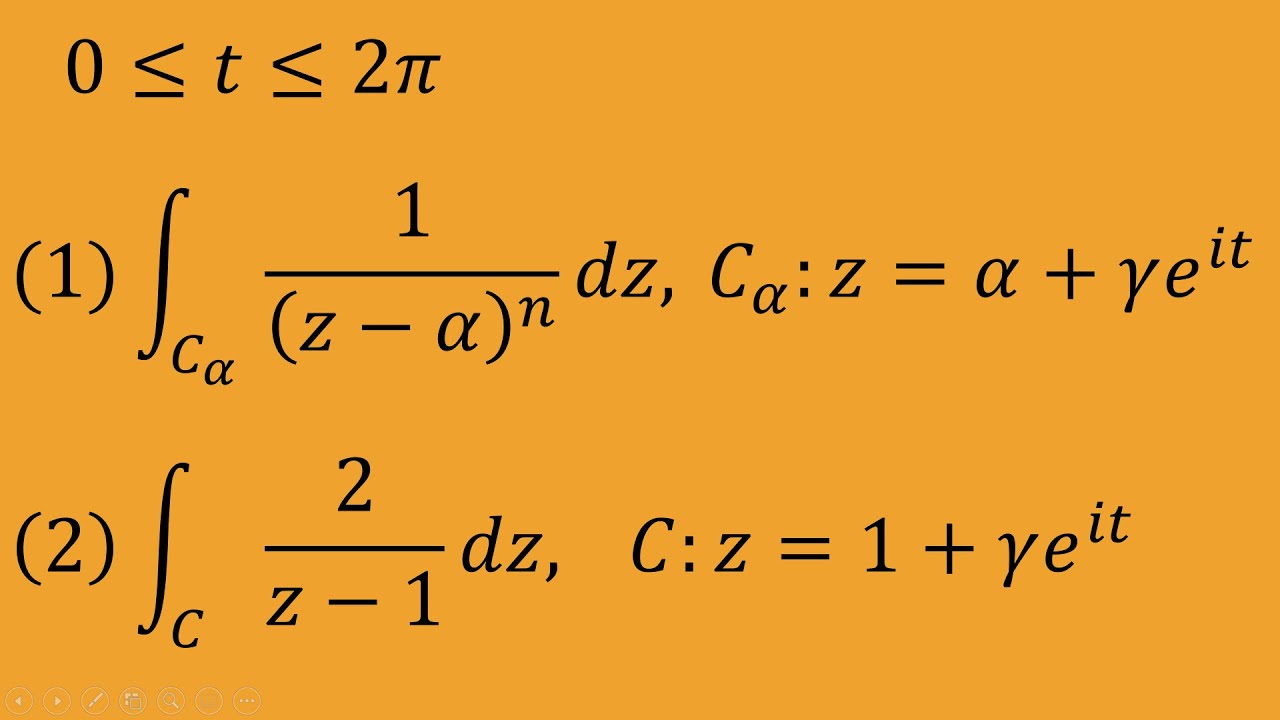07愛知県教員採用試験（数学：7番複素数） - 質問解決D.B.（データベース）

07愛知県教員採用試験（数学：7番　複素数）

問題文全文(内容文)：
$\boxed{7}$ $\vert Z \vert=1,Z^5=1$
$Z\leftarrow \in $を求めよ.

単元： #数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
$\boxed{7}$ $\vert Z \vert=1,Z^5=1$
$Z\leftarrow \in $を求めよ.

投稿日：2021.01.12

＜関連動画＞

神戸大　３次方程式の基本問題

単元： #数Ⅰ#数Ⅱ#数と式#複素数と方程式#複素数平面#一次不等式（不等式・絶対値のある方程式・不等式）#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C

指導講師：鈴木貫太郎

問題文全文(内容文)：
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.

神戸大過去問

この動画を見る　

京都大　複素数

単元： #数Ⅱ#複素数と方程式#複素数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$(1+i)^n+(1-i)^n \gt 10^{10}$をみたす最小の自然数$n$を求めよ.
$0.3 \lt \log_{10}2 \lt 0.302$

京大過去問

この動画を見る　

#7数検1級1次過去問複素数の方程式

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学検定#数学検定1級#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
$\boxed{2}$
$z=\in$とする.
$iz^2-4(1+2i)z+2(7+6i)=0$を解け.

この動画を見る　

久留米大（医）４次方程式

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
$x=1+\sqrt{3}c$が解である$x^4+ax^3+ax^2+(6-a)x+b=0$の
実数$a,b$を求めよ.

久留米大(医)過去問

この動画を見る　

20年5月数学検定準1級1次試験（複素数）

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学検定#数学検定準1級#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
$\boxed{4}$
$\alpha=(-1+i)(1-\sqrt3 i)$

(1)$\vert \alpha \vert $を求めよ.
(2)$arg \alpha$を求めよ.
$0\leqq arg \alpha \lt 2\pi$

20年5月数学検定準1級1次試験（複素数）過去問

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 07愛知県教員採用試験（数学：7番 複素数）

＜関連動画＞

神戸大 ３次方程式の基本問題

京都大 複素数

#7数検1級1次過去問 複素数の方程式

久留米大（医）４次方程式

20年5月数学検定準1級1次試験（複素数）