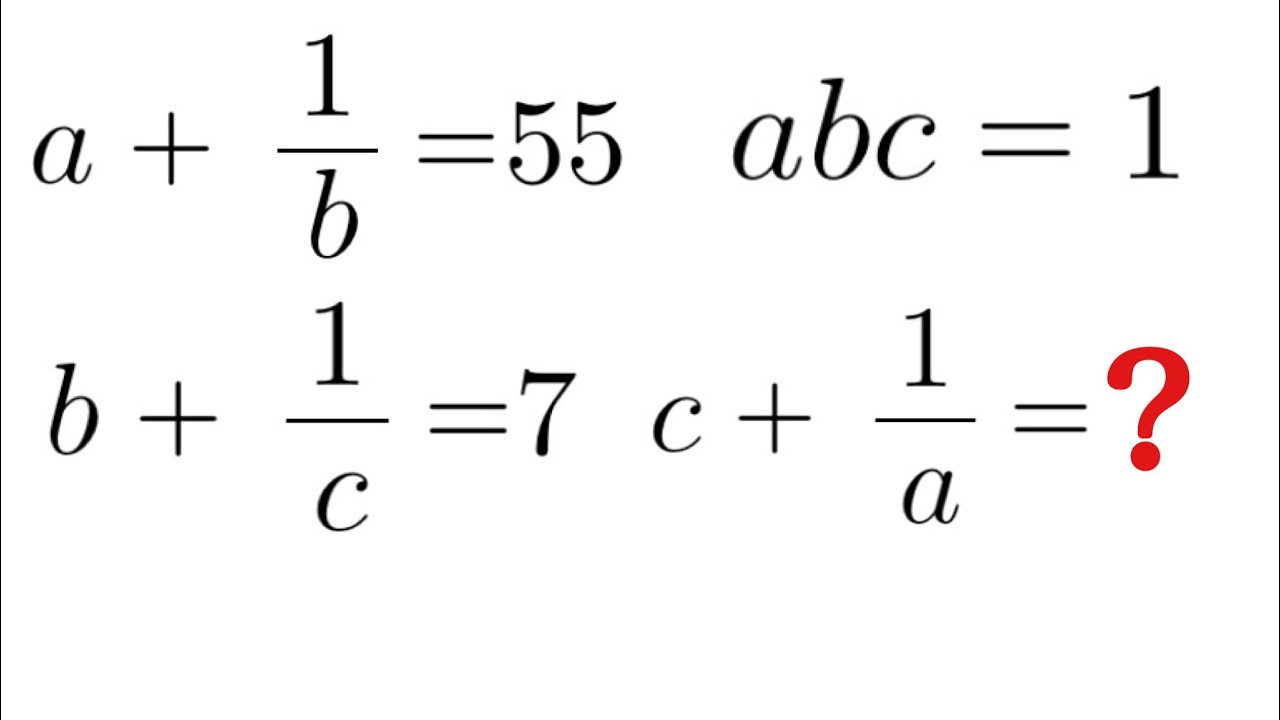問題文全文(内容文):
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
投稿日:2023.05.16