1次関数の文章題の解き方 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中２数学 > 1次関数 > 1次関数の文章題の解き方

1次関数の文章題の解き方

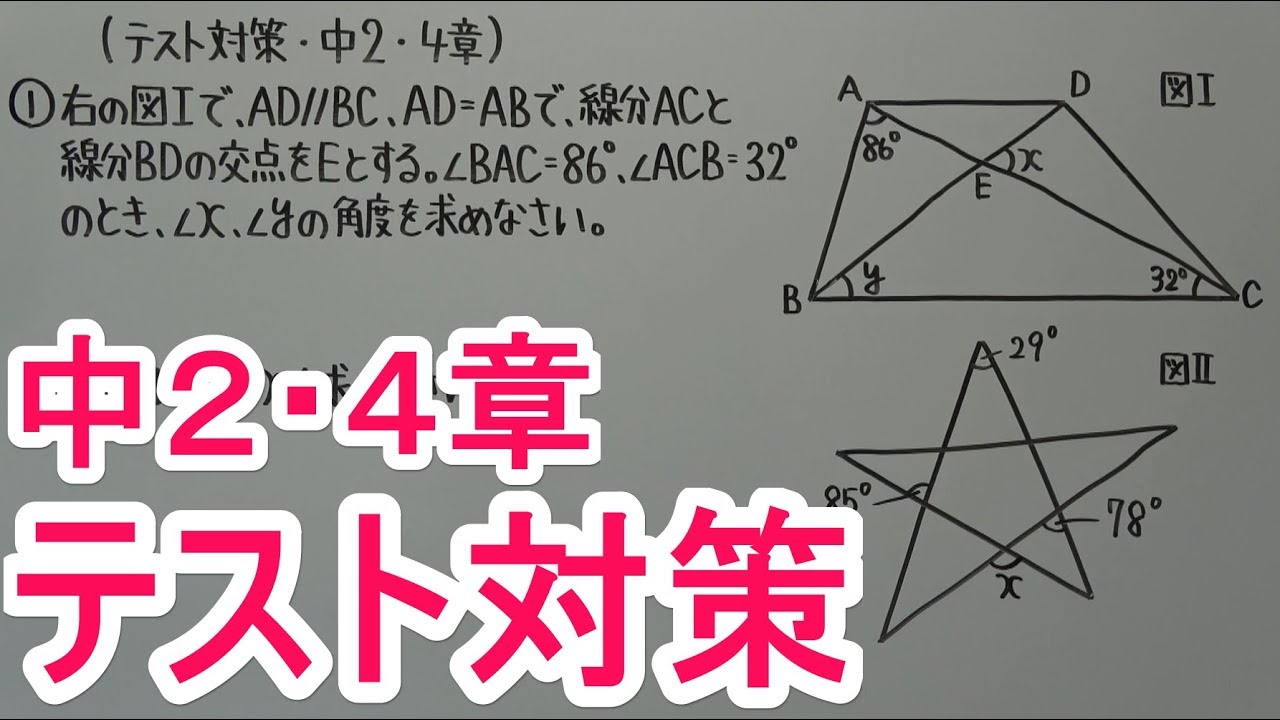
問題文全文(内容文)：
1次関数の文章題に関して解説していきます。
単元： #数学(中学生)#中２数学#1次関数#文章題#文章題その他
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1次関数の文章題に関して解説していきます。
投稿日：2025.11.24

＜関連動画＞

【中1数学/期末テスト対策】文字式の四則計算

アイキャッチ画像
単元： #数学(中学生)#中２数学#式の計算（単項式・多項式・式の四則計算）
指導講師： 【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
（1）$5a-3a$
（2）$x-3+3x+4$
（3）$4x\times(-3)$
（4）$12z\div(-4)$
この動画を見る　

【中２　数学】　　２－②②　連立方程式の利用（食塩水）

アイキャッチ画像
単元： #数学(中学生)#中２数学#連立方程式
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
中2 数学　連立方程式の利用（食塩水）
次の問に答えよ
① $190$ gの水に $10$ gの食塩をとかしたとき、食塩水の濃度は？
② $7$ %の食塩水 $300$ gにとけている食塩は？
③ $8$ %と $15$ %の食塩水をまぜて、$10$ %の食塩水を $700$ g作ります。
　それぞれ何g必要か？
この動画を見る　

【中学数学】1次関数：関数決定マスターへの道　8発目！　2点編Ⅰ

アイキャッチ画像
単元： #数学(中学生)#中２数学#1次関数
指導講師： 理数個別チャンネル
問題文全文(内容文)：
次の条件を満たす1次関数を求めよ。 x=3のときy=3、x=5のときy=7
この動画を見る　

9つの正方形と角の和

アイキャッチ画像
単元： #数学(中学生)#中２数学#数Ⅰ#数A#図形の性質#図形と計量#三角形と四角形#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
$\angle a + \angle b +\angle c=? $
＊図は動画内参照
この動画を見る　

【数学】確率の求め方間違っていませんか？確率の前提の話　前編

アイキャッチ画像
単元： #数学(中学生)#中２数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師： 理数個別チャンネル
問題文全文(内容文)：
確率の求め方で、間違った数え方していませんか？
確率の計算方法について解説します。

大小二つのサイコロを振った時、目の合計が3になる確率は？
二つのサイコロを振った時、目の合計が3になる確率は？

答えに違いはある？？
この動画を見る　
トップへ戻る