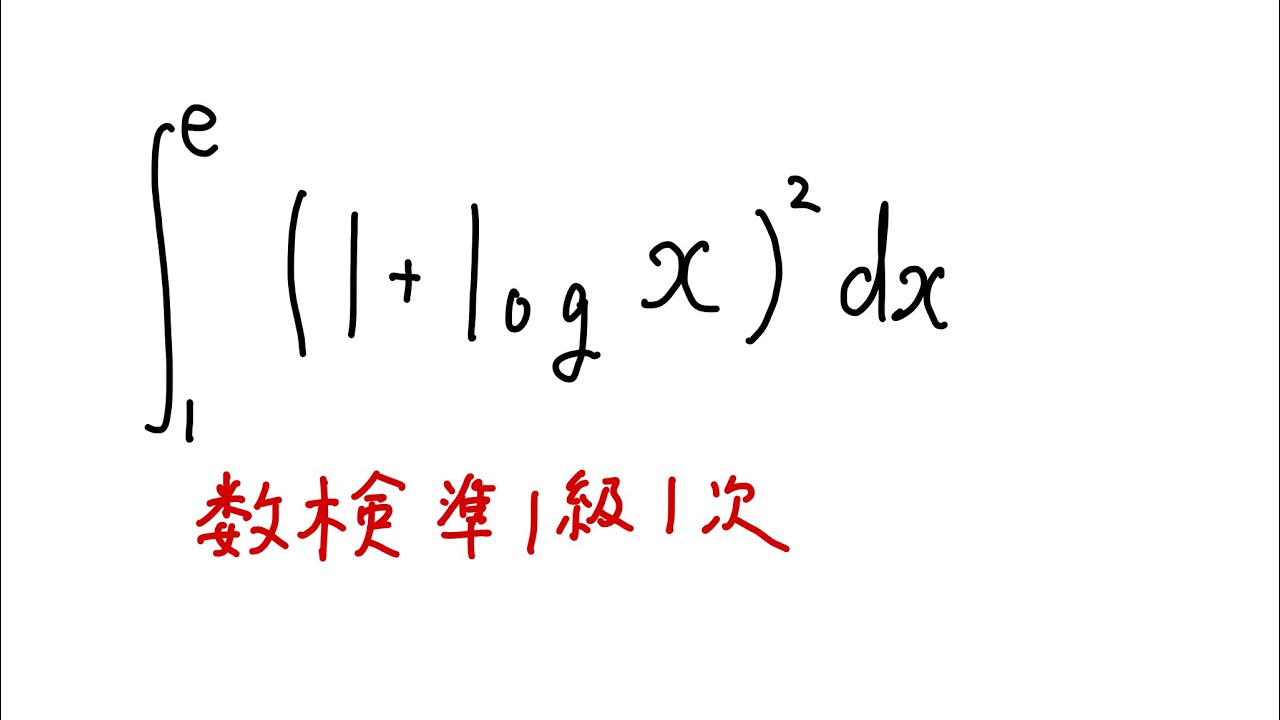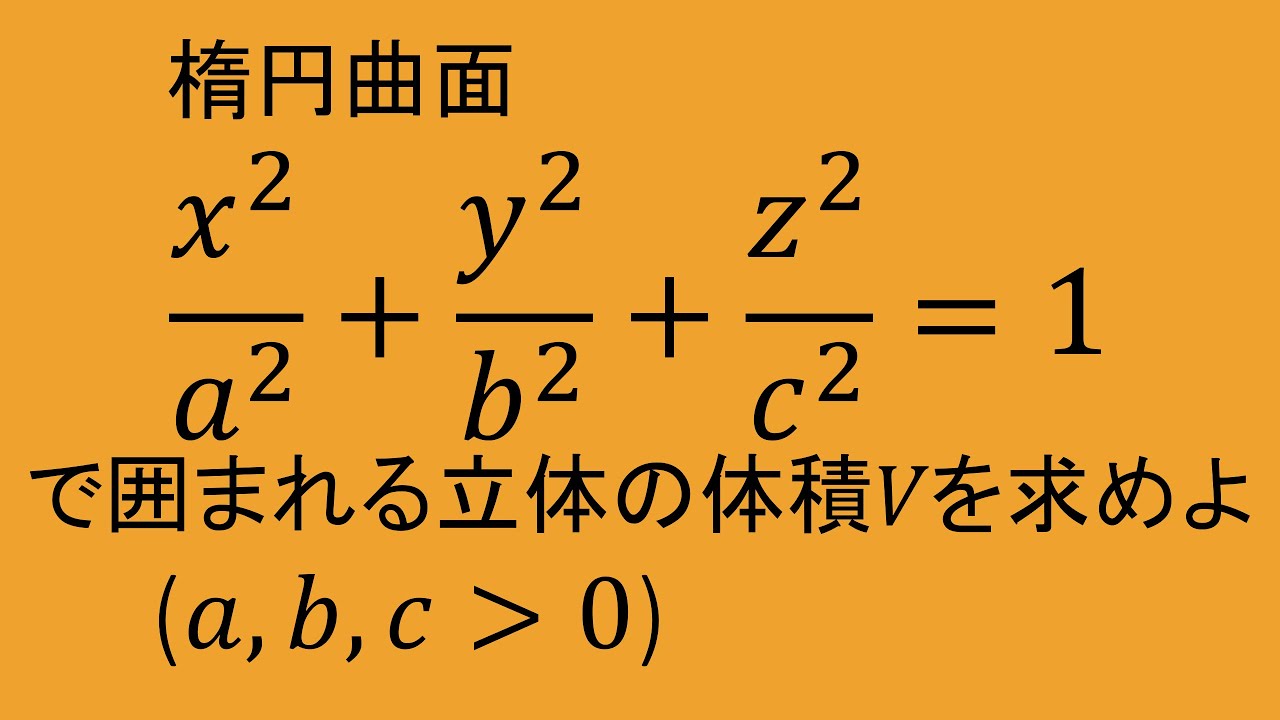問題文全文(内容文):
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
①$2ab+c^2\gt 150$ ②$2ab+c^2\geqq 150$ ③$2ab+c^2\lt 150$
④$2ab+c^2\leqq 150$ ⑤a^2b^2+c^2\lt 150$ ⑥$a^2b^2+c^2\leqq 150$
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
①$2ab+c^2\gt 150$ ②$2ab+c^2\geqq 150$ ③$2ab+c^2\lt 150$
④$2ab+c^2\leqq 150$ ⑤a^2b^2+c^2\lt 150$ ⑥$a^2b^2+c^2\leqq 150$
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
チャプター:
0:00 数学検定3級の出題範囲について
0:29 (1)の解説
1:11 (2)の解説
2:24 (3)の解説
4:23 (4)の解説
5:22 まとめ
単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
①$2ab+c^2\gt 150$ ②$2ab+c^2\geqq 150$ ③$2ab+c^2\lt 150$
④$2ab+c^2\leqq 150$ ⑤a^2b^2+c^2\lt 150$ ⑥$a^2b^2+c^2\leqq 150$
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
①$2ab+c^2\gt 150$ ②$2ab+c^2\geqq 150$ ③$2ab+c^2\lt 150$
④$2ab+c^2\leqq 150$ ⑤a^2b^2+c^2\lt 150$ ⑥$a^2b^2+c^2\leqq 150$
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
投稿日:2022.09.23