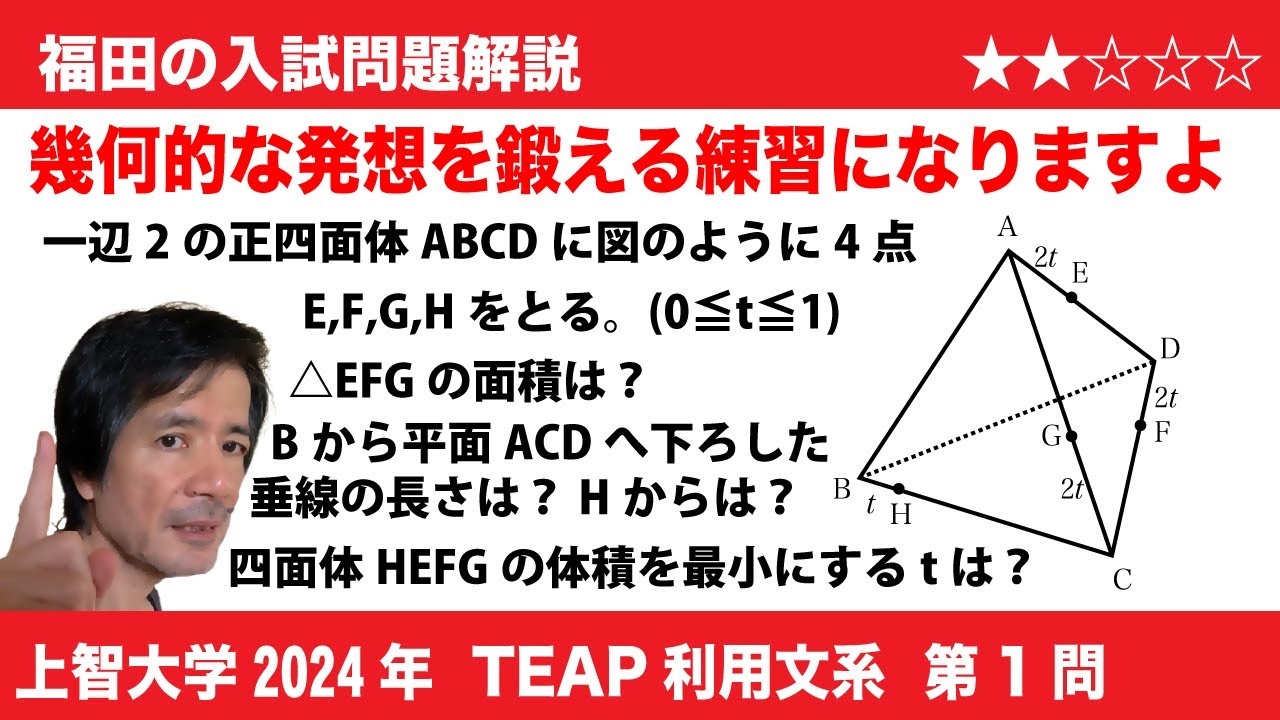
問題文全文(内容文):
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
投稿日:2023.04.01