問題文全文(内容文):
高校受験対策・難解死守3
①方程式$\frac{2x-3}{4}=\frac{x+2}{3}$を解け。
➁$\frac{x-6}{8}-0.75=\frac{1}{2}x$を解け
③$a^2-2b^2-ab+bc+ca$を因数分解せよ。
④$\sqrt{n^2+55}$が自然数となるような自然数$n$の値をすべて求めよ。
⑤
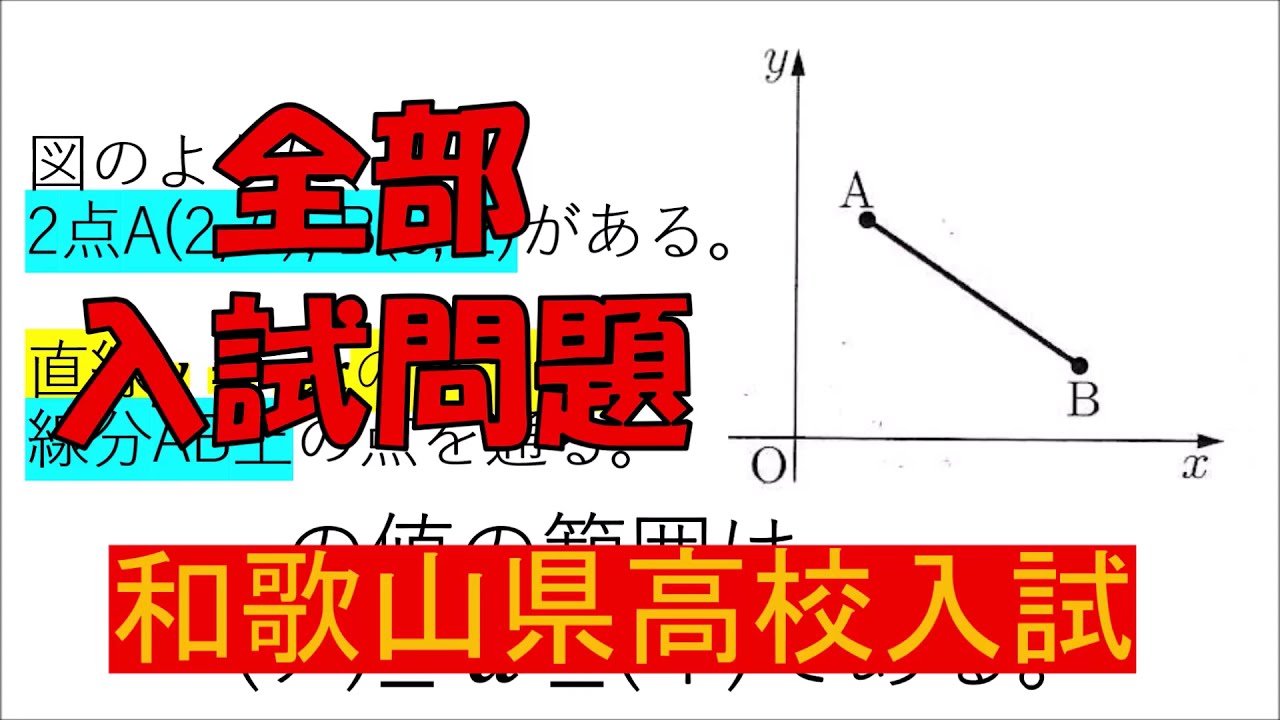
右の図のような台形$ABCD$があり、点$E$は辺$AB$の中点である。
また、線分$ED$上に点$F$を$EF:FD=2:5$となるようにとる。
このとき、$△ECF$の面積は台形$ABCD$の面積の何倍になるか求めよ。
⑥
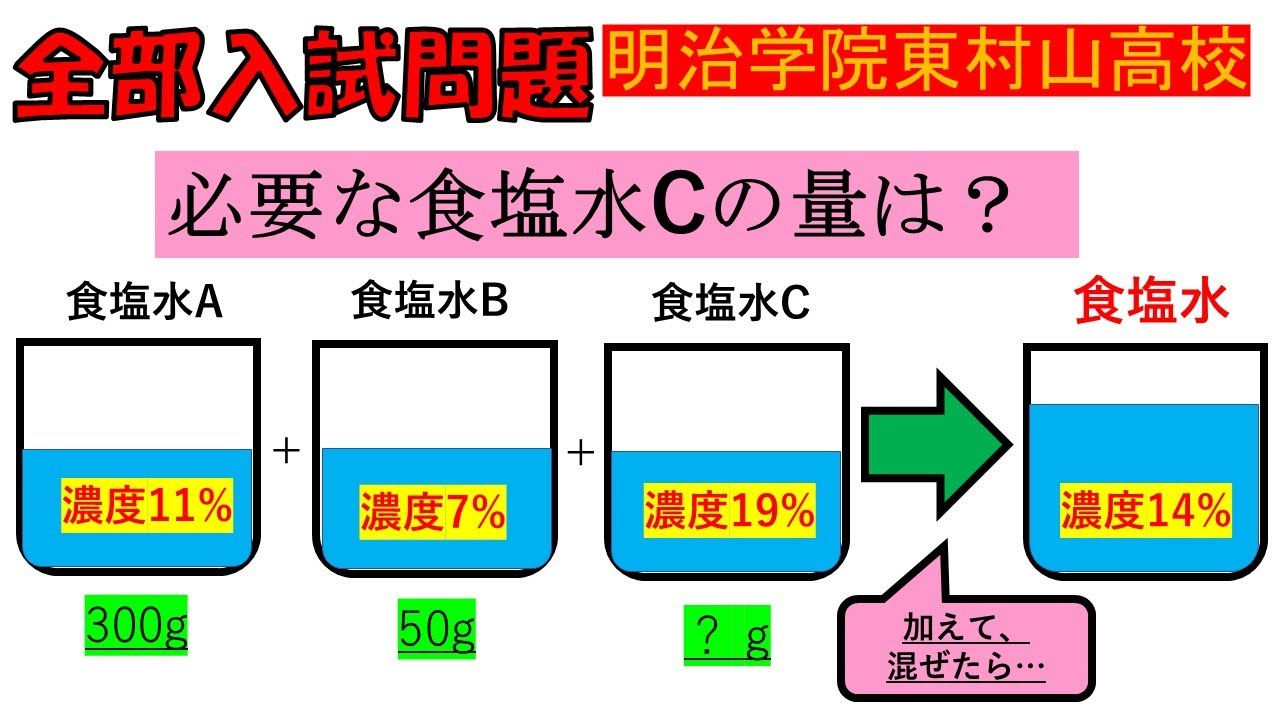
3桁の正の整数$N$がある。
$N$を100で割った余りは百の位の数を12倍した数に1加えた数に等しい。
また、$N$の一の位の数を十の位に、$N$の十の位の数を百の位に、
$N$の百の位の数を一の位にそれぞれ置きかえてできる数はもとの整数$N$より63大きい。
このとき正の整数$N$を求めよ。
高校受験対策・難解死守3
①方程式$\frac{2x-3}{4}=\frac{x+2}{3}$を解け。
➁$\frac{x-6}{8}-0.75=\frac{1}{2}x$を解け
③$a^2-2b^2-ab+bc+ca$を因数分解せよ。
④$\sqrt{n^2+55}$が自然数となるような自然数$n$の値をすべて求めよ。
⑤
右の図のような台形$ABCD$があり、点$E$は辺$AB$の中点である。
また、線分$ED$上に点$F$を$EF:FD=2:5$となるようにとる。
このとき、$△ECF$の面積は台形$ABCD$の面積の何倍になるか求めよ。
⑥
3桁の正の整数$N$がある。
$N$を100で割った余りは百の位の数を12倍した数に1加えた数に等しい。
また、$N$の一の位の数を十の位に、$N$の十の位の数を百の位に、
$N$の百の位の数を一の位にそれぞれ置きかえてできる数はもとの整数$N$より63大きい。
このとき正の整数$N$を求めよ。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・難解死守3
①方程式$\frac{2x-3}{4}=\frac{x+2}{3}$を解け。
➁$\frac{x-6}{8}-0.75=\frac{1}{2}x$を解け
③$a^2-2b^2-ab+bc+ca$を因数分解せよ。
④$\sqrt{n^2+55}$が自然数となるような自然数$n$の値をすべて求めよ。
⑤
右の図のような台形$ABCD$があり、点$E$は辺$AB$の中点である。
また、線分$ED$上に点$F$を$EF:FD=2:5$となるようにとる。
このとき、$△ECF$の面積は台形$ABCD$の面積の何倍になるか求めよ。
⑥
3桁の正の整数$N$がある。
$N$を100で割った余りは百の位の数を12倍した数に1加えた数に等しい。
また、$N$の一の位の数を十の位に、$N$の十の位の数を百の位に、
$N$の百の位の数を一の位にそれぞれ置きかえてできる数はもとの整数$N$より63大きい。
このとき正の整数$N$を求めよ。
高校受験対策・難解死守3
①方程式$\frac{2x-3}{4}=\frac{x+2}{3}$を解け。
➁$\frac{x-6}{8}-0.75=\frac{1}{2}x$を解け
③$a^2-2b^2-ab+bc+ca$を因数分解せよ。
④$\sqrt{n^2+55}$が自然数となるような自然数$n$の値をすべて求めよ。
⑤
右の図のような台形$ABCD$があり、点$E$は辺$AB$の中点である。
また、線分$ED$上に点$F$を$EF:FD=2:5$となるようにとる。
このとき、$△ECF$の面積は台形$ABCD$の面積の何倍になるか求めよ。
⑥
3桁の正の整数$N$がある。
$N$を100で割った余りは百の位の数を12倍した数に1加えた数に等しい。
また、$N$の一の位の数を十の位に、$N$の十の位の数を百の位に、
$N$の百の位の数を一の位にそれぞれ置きかえてできる数はもとの整数$N$より63大きい。
このとき正の整数$N$を求めよ。
投稿日:2020.01.21