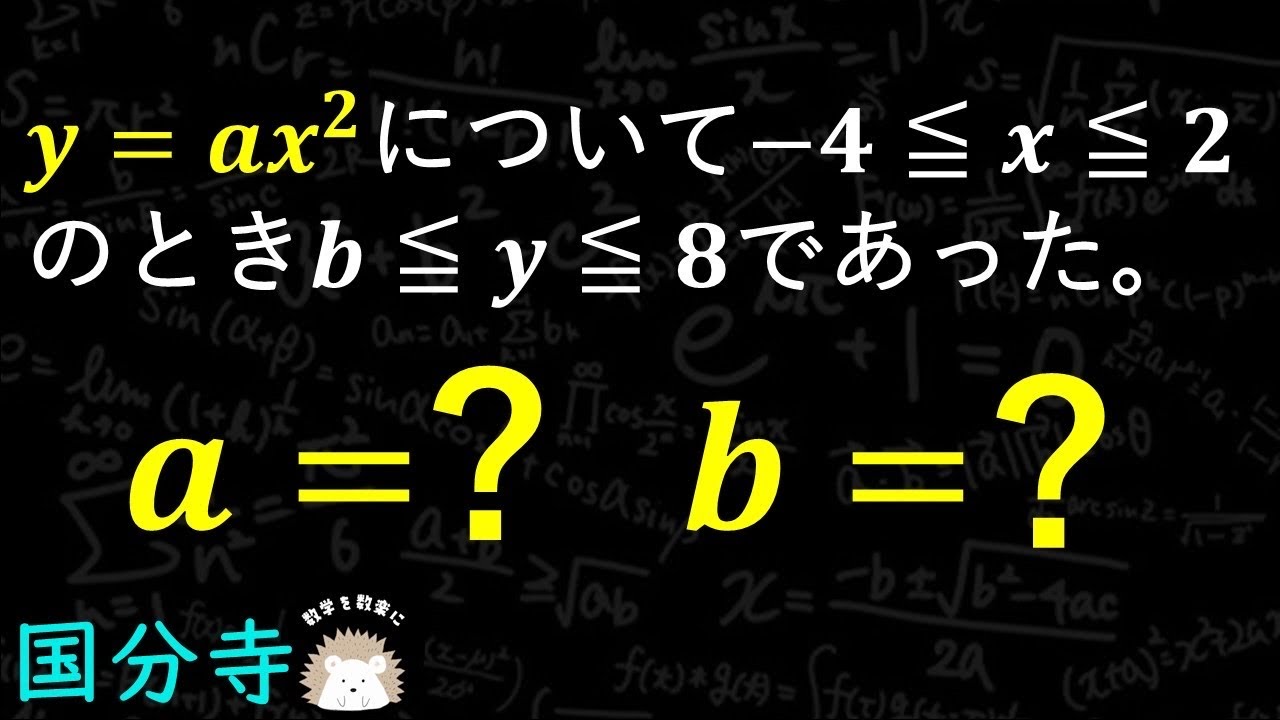【数Ⅰ】【図形と計量】測量への応用2 ※問題文は概要欄

問題文全文(内容文)：
建物の高さ PQ を知るために，地点Qの真西の地点Aから屋上Pの仰角を測ったら 45°，真南の地点BからPの仰角を測ったら 30°，AB間の距離を測ったら20mであった。建物の高さを求めよ。

チャプター：

■チャプター
0:00 オープニング
0:06 解説開始！まずは問題整理
0:56 AQの長さを出す！
1:31 QBの長さを出す！
2:13 △AQBの形って？
4:21 ラスト！xの長さを出す！

単元： #数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)

教材： #4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材

指導講師：理数個別チャンネル

投稿日：2024.11.11

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$x=\sqrt{2023}$のとき
$x^2-89x+1980$の値について正しいのは？
①符号は正である
②符号は負である
③0である

函館ラ・サール高等学校

この動画を見る　

単元： #図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
三角比の相互関係の公式の証明について解説していきます。

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
(1) x³+x²y-x²-y

(2) 2x²+5xy+3y²-3x-5y-2

(3) a(b²-c²)+b(c²-a²)+c(a²-b²)

この動画を見る　

単元： #数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$x=1+\sqrt 2 + \sqrt 3 + \sqrt 5$のとき
$x^2-2x+5$の値は？
大阪星光学院2024

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
a= 9999のとき
$\frac{4a^3 - a }{(2a+1)(6a-3)} = ?$

この動画を見る　