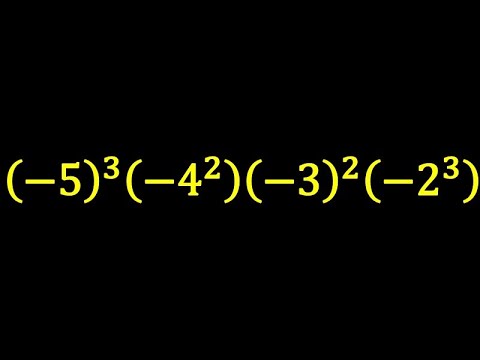問題文全文(内容文):
高校受験対策・関数51
Q
妹と兄は、家から2310mはなれた図書館へ行きました。
妹は歩いて家を出発し、一定の速さで進み、25分後に家から1500mはなれた地点を通過し、図書館まで行きました。
兄は妹が家を出発してから20分後に自転車で家を出発し、一定の速さで進み、その5分後に家から
700mはなれた地点に着きました。
右の図は、妹が家を出発してからの時間を$x$ 分、家からの道のりを$y$ mとしたとき、妹・兄それぞれの$x$と$y$の関係をグラフに表したものです。
兄のグラフはそのときのようすを途中まで表しています。
①兄のグラフの傾きを求めなさい。
②兄は妹が家を出発してから25分後に自転車が故障し、 少しの間立ち止まってしまいました。
その後、故障前と同じ一定 の速さで進んだところ、妹と同時に図書館に着きました。
兄が立ち止まっていた時間は何分間ですか。その時間を求めなさい。
高校受験対策・関数51
Q
妹と兄は、家から2310mはなれた図書館へ行きました。
妹は歩いて家を出発し、一定の速さで進み、25分後に家から1500mはなれた地点を通過し、図書館まで行きました。
兄は妹が家を出発してから20分後に自転車で家を出発し、一定の速さで進み、その5分後に家から
700mはなれた地点に着きました。
右の図は、妹が家を出発してからの時間を$x$ 分、家からの道のりを$y$ mとしたとき、妹・兄それぞれの$x$と$y$の関係をグラフに表したものです。
兄のグラフはそのときのようすを途中まで表しています。
①兄のグラフの傾きを求めなさい。
②兄は妹が家を出発してから25分後に自転車が故障し、 少しの間立ち止まってしまいました。
その後、故障前と同じ一定 の速さで進んだところ、妹と同時に図書館に着きました。
兄が立ち止まっていた時間は何分間ですか。その時間を求めなさい。
単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数51
Q
妹と兄は、家から2310mはなれた図書館へ行きました。
妹は歩いて家を出発し、一定の速さで進み、25分後に家から1500mはなれた地点を通過し、図書館まで行きました。
兄は妹が家を出発してから20分後に自転車で家を出発し、一定の速さで進み、その5分後に家から
700mはなれた地点に着きました。
右の図は、妹が家を出発してからの時間を$x$ 分、家からの道のりを$y$ mとしたとき、妹・兄それぞれの$x$と$y$の関係をグラフに表したものです。
兄のグラフはそのときのようすを途中まで表しています。
①兄のグラフの傾きを求めなさい。
②兄は妹が家を出発してから25分後に自転車が故障し、 少しの間立ち止まってしまいました。
その後、故障前と同じ一定 の速さで進んだところ、妹と同時に図書館に着きました。
兄が立ち止まっていた時間は何分間ですか。その時間を求めなさい。
高校受験対策・関数51
Q
妹と兄は、家から2310mはなれた図書館へ行きました。
妹は歩いて家を出発し、一定の速さで進み、25分後に家から1500mはなれた地点を通過し、図書館まで行きました。
兄は妹が家を出発してから20分後に自転車で家を出発し、一定の速さで進み、その5分後に家から
700mはなれた地点に着きました。
右の図は、妹が家を出発してからの時間を$x$ 分、家からの道のりを$y$ mとしたとき、妹・兄それぞれの$x$と$y$の関係をグラフに表したものです。
兄のグラフはそのときのようすを途中まで表しています。
①兄のグラフの傾きを求めなさい。
②兄は妹が家を出発してから25分後に自転車が故障し、 少しの間立ち止まってしまいました。
その後、故障前と同じ一定 の速さで進んだところ、妹と同時に図書館に着きました。
兄が立ち止まっていた時間は何分間ですか。その時間を求めなさい。
投稿日:2020.12.20