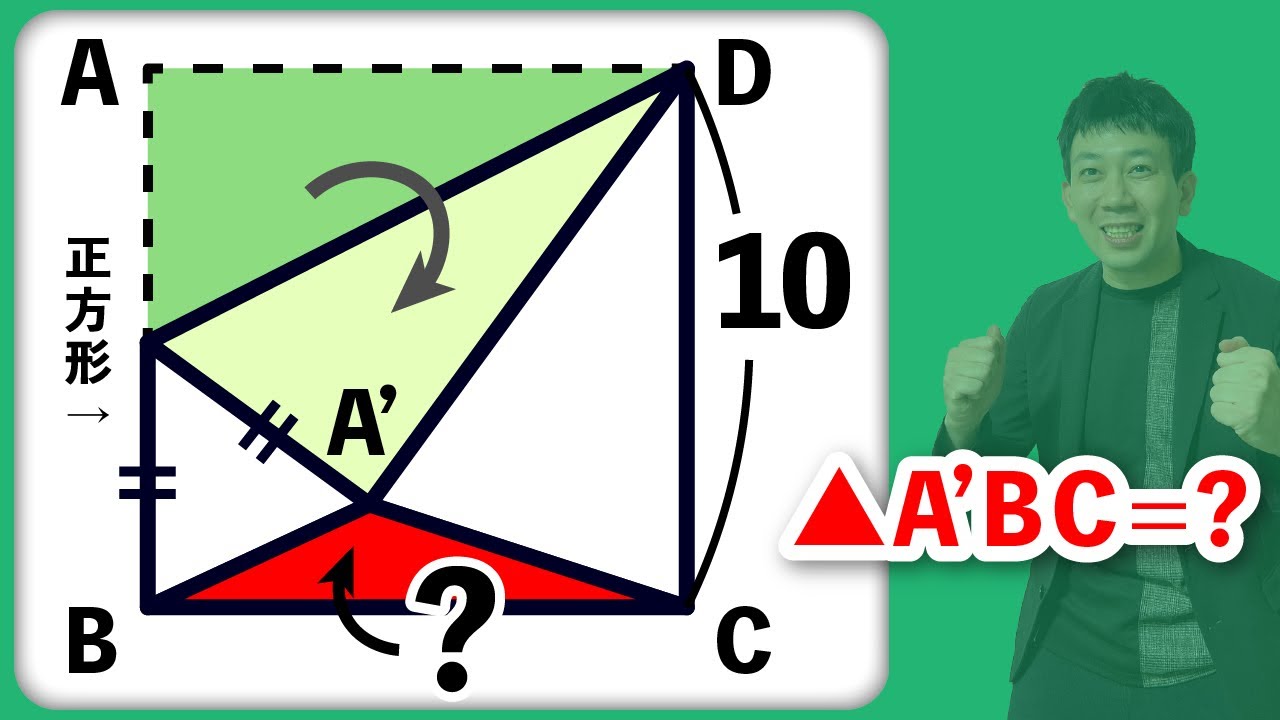
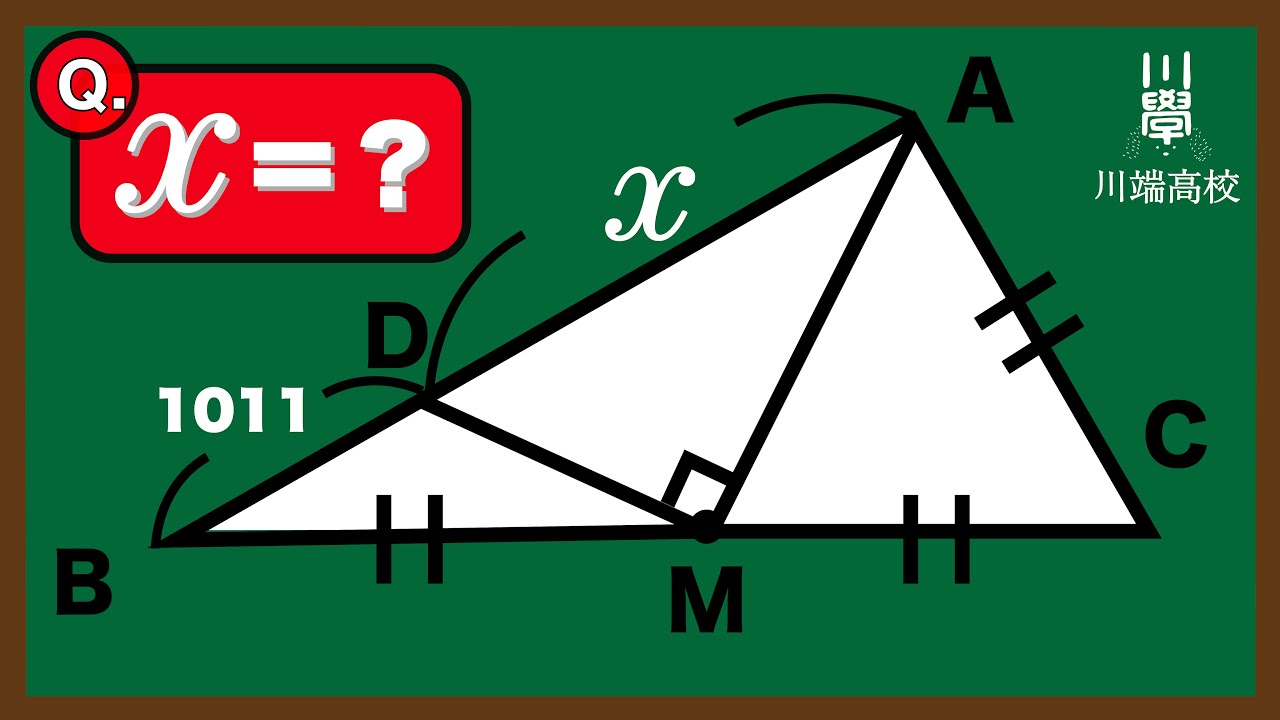
問題文全文(内容文):
入試問題 三重県の高校
あとの問いに答えなさい。
サイズが異なるさいころを同時に1回投げ、
$2$桁の整数$m:$
十の位: さいころ大の出た目
一の位: さいころ小の出た目
$m$が素数となる確率を求めなさい。
※さいころの目は$1,2,3,4,5,6$であり、
どの目が出ることも同様に確からしい
入試問題 三重県の高校
あとの問いに答えなさい。
サイズが異なるさいころを同時に1回投げ、
$2$桁の整数$m:$
十の位: さいころ大の出た目
一の位: さいころ小の出た目
$m$が素数となる確率を求めなさい。
※さいころの目は$1,2,3,4,5,6$であり、
どの目が出ることも同様に確からしい
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#三重県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 三重県の高校
あとの問いに答えなさい。
サイズが異なるさいころを同時に1回投げ、
$2$桁の整数$m:$
十の位: さいころ大の出た目
一の位: さいころ小の出た目
$m$が素数となる確率を求めなさい。
※さいころの目は$1,2,3,4,5,6$であり、
どの目が出ることも同様に確からしい
入試問題 三重県の高校
あとの問いに答えなさい。
サイズが異なるさいころを同時に1回投げ、
$2$桁の整数$m:$
十の位: さいころ大の出た目
一の位: さいころ小の出た目
$m$が素数となる確率を求めなさい。
※さいころの目は$1,2,3,4,5,6$であり、
どの目が出ることも同様に確からしい
投稿日:2020.11.13