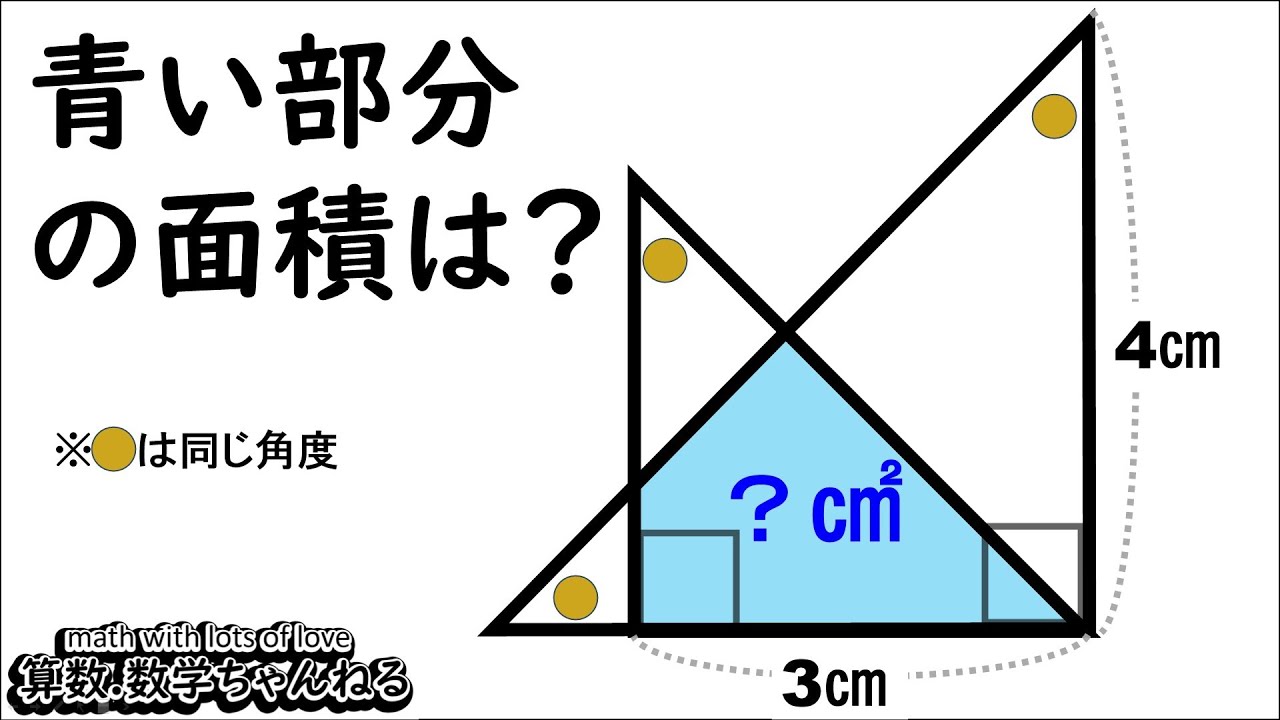
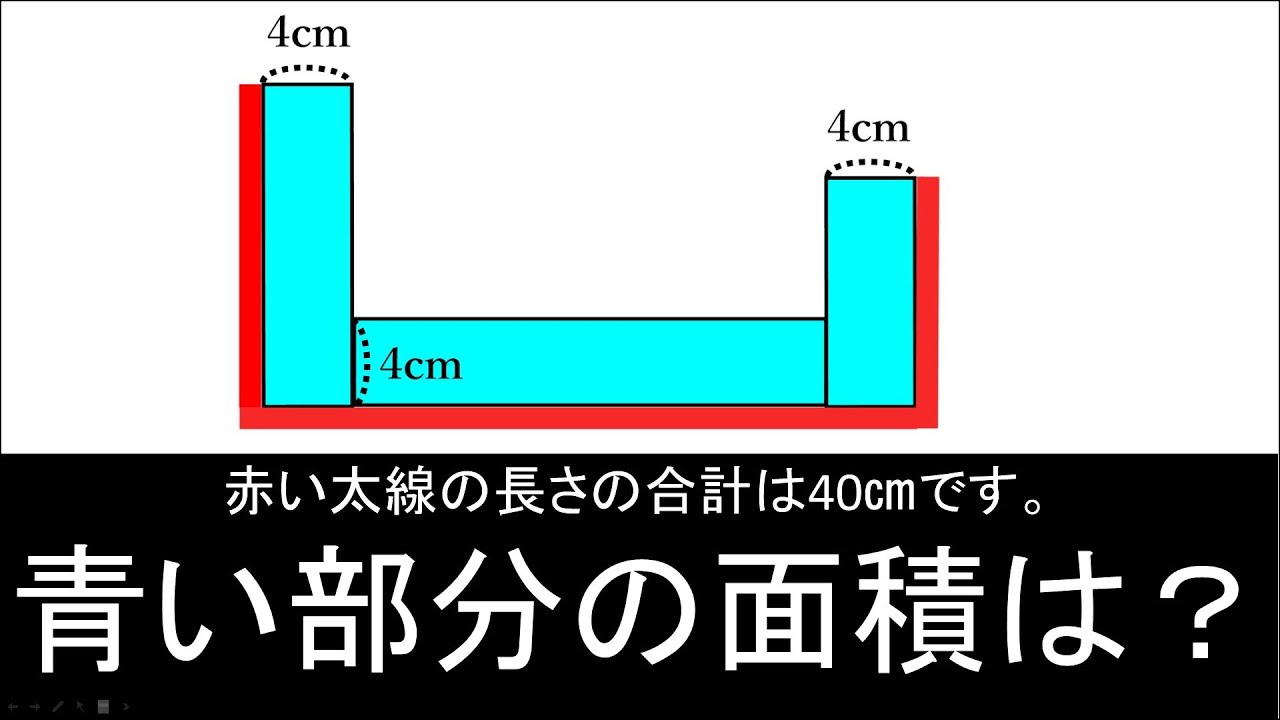
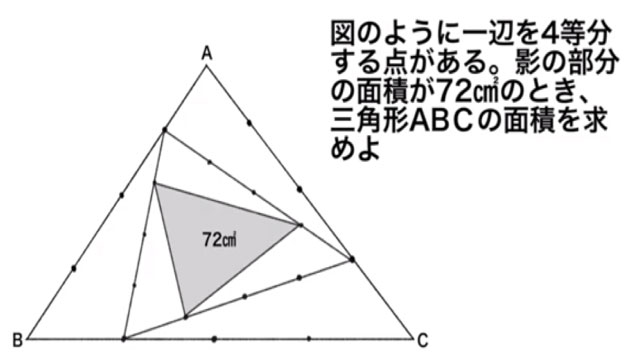
問題文全文(内容文):
右図のような台形ABCDがあります。点PはBを出発し、秒速2cmでA、Dを通ってCま で進みます。
(1)点PがBを出発してから3秒後の三角形PBCの面積を求めよう。
(2) 三角形PBCの面積が最大になるのは何秒後から何秒後までですか。
(3)三角形PBC の面積がはじめて320cm²になるのは、点PがBを出発してから何秒後ですか。
(4) 三角形PBCの面積が2度目に320cm²になるのは、点PがBを出発してから何秒後ですか。
右図のような台形ABCDがあります。点PはBを出発し、秒速2cmでA、Dを通ってCま で進みます。
(1)点PがBを出発してから3秒後の三角形PBCの面積を求めよう。
(2) 三角形PBCの面積が最大になるのは何秒後から何秒後までですか。
(3)三角形PBC の面積がはじめて320cm²になるのは、点PがBを出発してから何秒後ですか。
(4) 三角形PBCの面積が2度目に320cm²になるのは、点PがBを出発してから何秒後ですか。
チャプター:
0:00 オープニング
0:05 問題文
0:20 点Pの情報整理
0:30 問題解説(1):点Pの移動距離は?
1:10 問題解説(2):面積最大=高さ最大
2:06 問題解説(3):面積から高さは?
3:18 問題解説(4):平行は比が同じ
4:34 名言
単元:
#算数(中学受験)#速さ#点の移動・時計算
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のような台形ABCDがあります。点PはBを出発し、秒速2cmでA、Dを通ってCま で進みます。
(1)点PがBを出発してから3秒後の三角形PBCの面積を求めよう。
(2) 三角形PBCの面積が最大になるのは何秒後から何秒後までですか。
(3)三角形PBC の面積がはじめて320cm²になるのは、点PがBを出発してから何秒後ですか。
(4) 三角形PBCの面積が2度目に320cm²になるのは、点PがBを出発してから何秒後ですか。
右図のような台形ABCDがあります。点PはBを出発し、秒速2cmでA、Dを通ってCま で進みます。
(1)点PがBを出発してから3秒後の三角形PBCの面積を求めよう。
(2) 三角形PBCの面積が最大になるのは何秒後から何秒後までですか。
(3)三角形PBC の面積がはじめて320cm²になるのは、点PがBを出発してから何秒後ですか。
(4) 三角形PBCの面積が2度目に320cm²になるのは、点PがBを出発してから何秒後ですか。
投稿日:2021.06.19