福田のおもしろ数学022〜10秒でできたら天才〜2つの円と線分 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中２数学 > 三角形と四角形 > 福田のおもしろ数学022〜10秒でできたら天才〜2つの円と線分

福田のおもしろ数学022〜10秒でできたら天才〜2つの円と線分

問題文全文(内容文)：
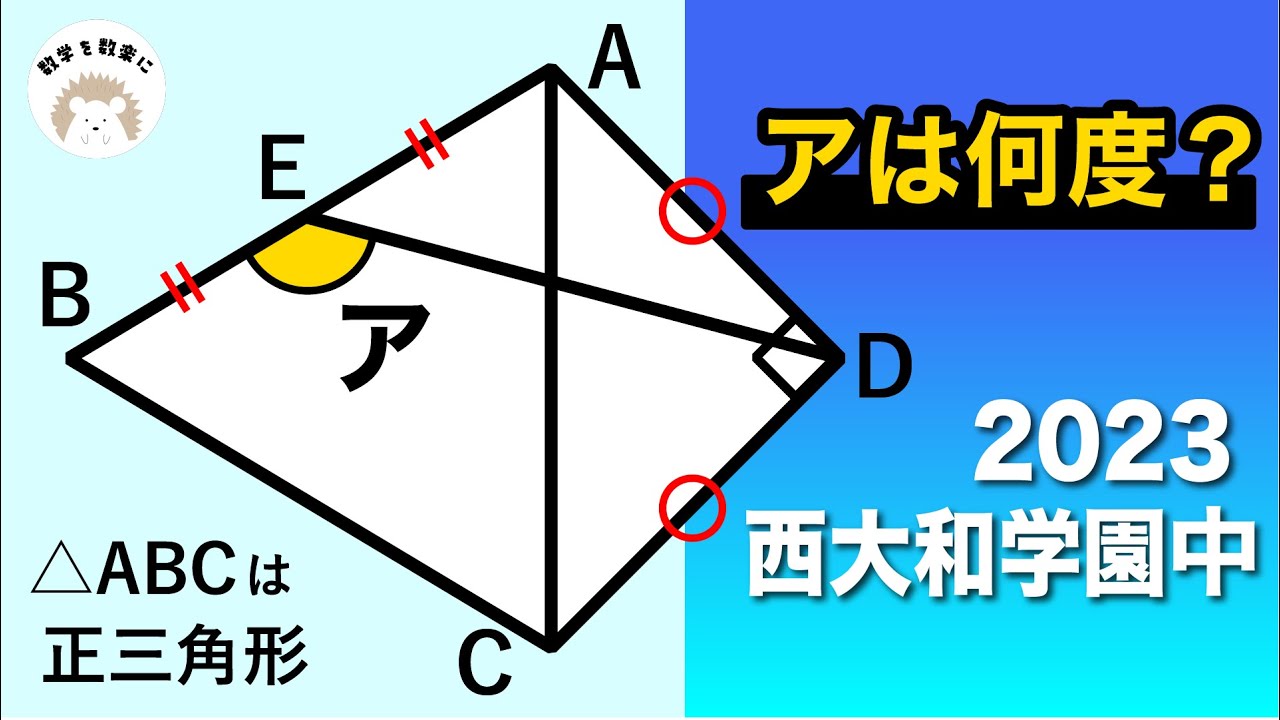
Xを求めよ。
※図は動画内参照
単元： #中２数学#数A#図形の性質#方べきの定理と２つの円の関係#三角形と四角形#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
Xを求めよ。
※図は動画内参照
投稿日：2024.01.17

＜関連動画＞

三角形の回転　四天王寺高校2022年入試問題解説48問目

アイキャッチ画像
単元： #数学(中学生)#中２数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
△ABCを頂点Cを中心として、反時計回りに一回点させる時
辺ABが通過してできる図形の面積は？
＊図は動画内参照

2022四天王寺高等学校
この動画を見る　

【テスト対策 中2】6章-4

アイキャッチ画像
単元： #数学(中学生)#中２数学#確率
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
①当たりが3本入った5本のくじがある。
このくじを$A、B$の2人がこの順に1本ずつ引くとき
2人とも当たりを引く確率を求めなさい。
ただし、引いたくじは戻さないものとする。

◎当たりが4本入った10本のくじについて次の問いに答えなさい。
引いたくじは戻さないものとする。

②A君が同時に2本引くとき、2本ともはずれを引く確率を求めなさい。

③A君が同時に2本引き、そのあとにBさんが1本引くとき、
Bさんだけが当たりを引く確率を求めなさい。
この動画を見る　

【裏技】学校では教えてもらえない技

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中１数学#中２数学#中３数学#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
8000のようなキリのいい数字に使えるひっ算の簡単計算方法紹介動画です
この動画を見る　

ビッグマックのチーズの値段ってなんぼ？

アイキャッチ画像
単元： #数学(中学生)#中２数学#連立方程式
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
ビッグマックを使って数学的に解説
この動画を見る　

算数　3通りの解説　

アイキャッチ画像
単元： #算数(中学受験)#数学(中学生)#中２数学#平面図形#角度と面積#三角形と四角形
指導講師： 数学を数楽に
問題文全文(内容文)：
長方形の面積は？
＊図は動画内参照
この動画を見る　
Back to top