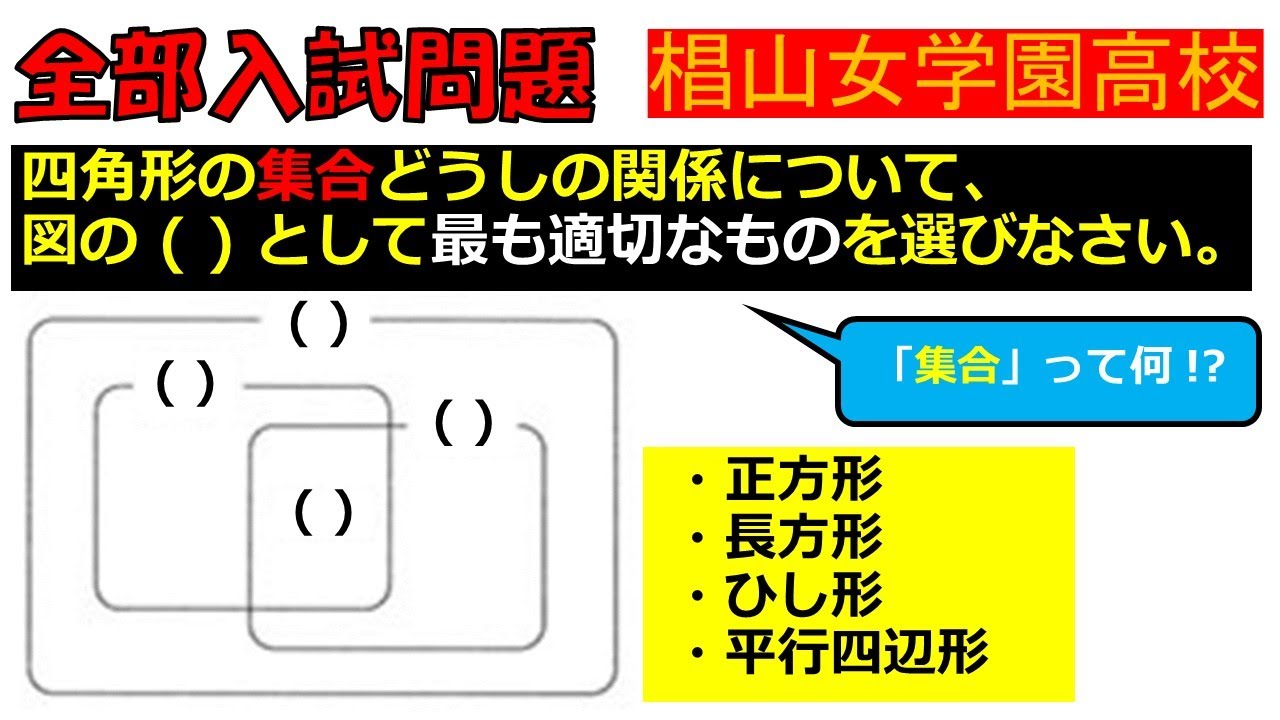
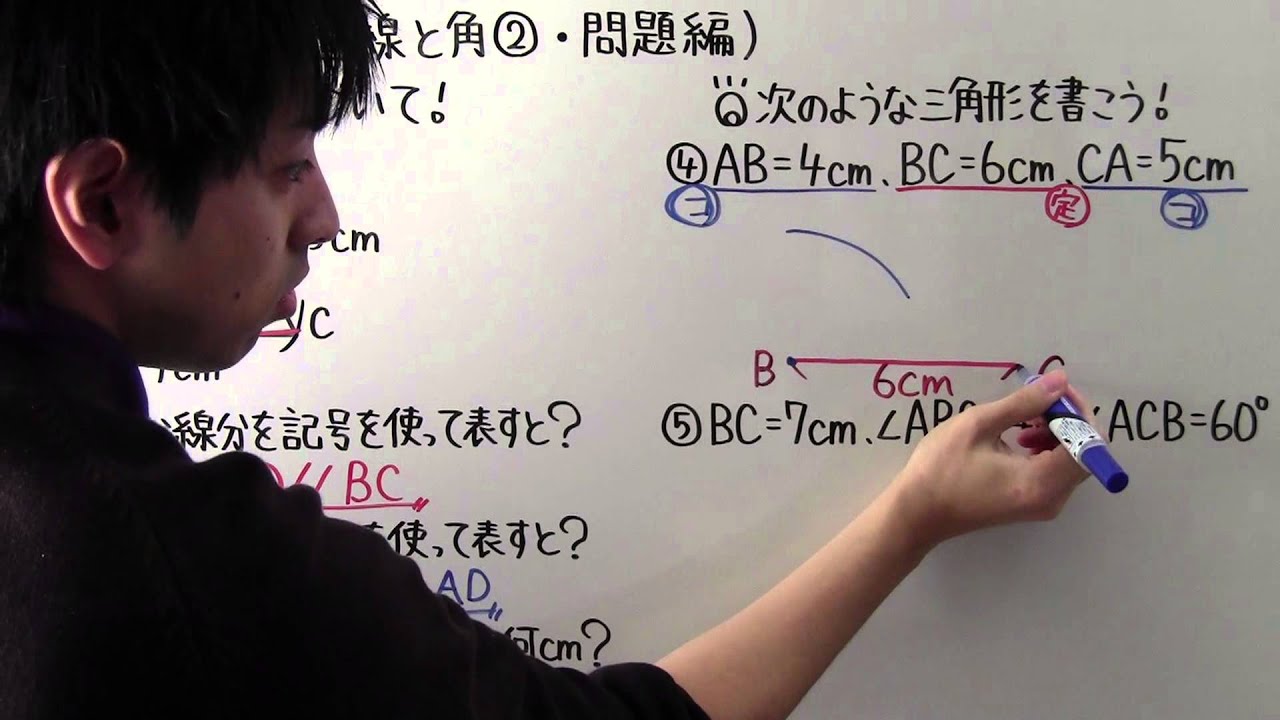
問題文全文(内容文):
二等辺三角形において成り立つ性質の証明を行います。
二等辺三角形において成り立つ性質の証明を行います。
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
二等辺三角形において成り立つ性質の証明を行います。
二等辺三角形において成り立つ性質の証明を行います。
投稿日:2023.01.16