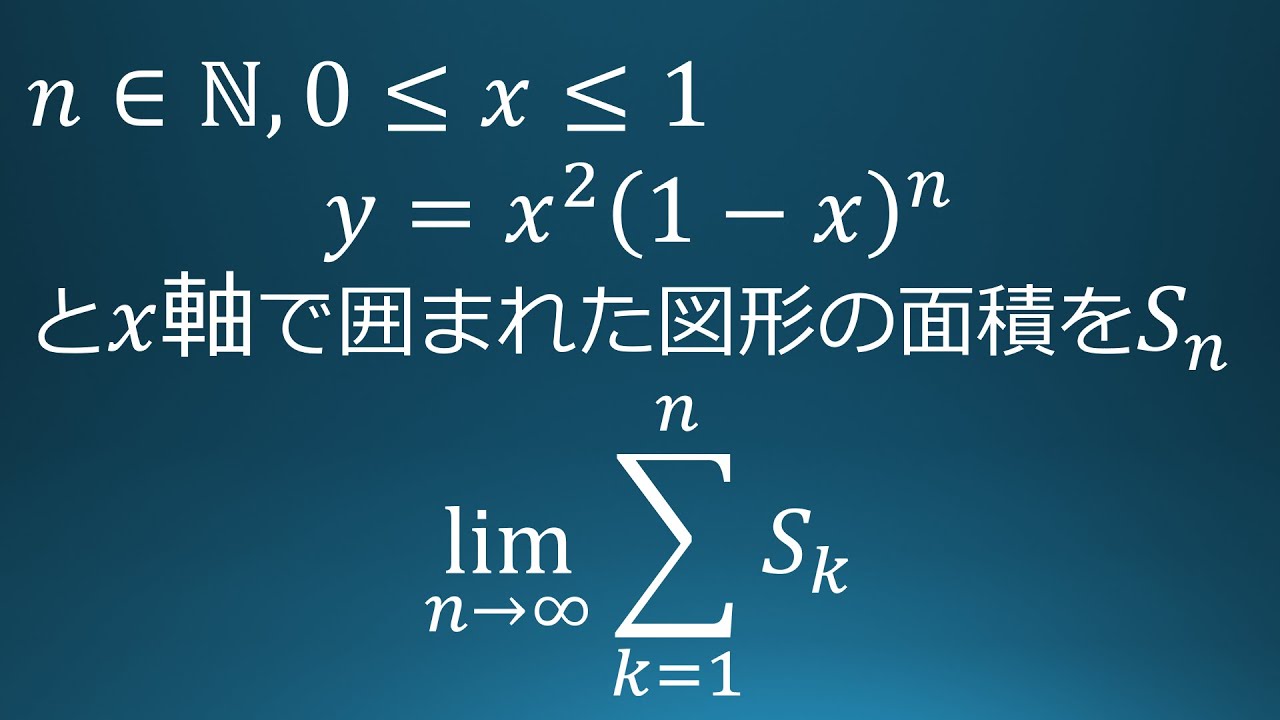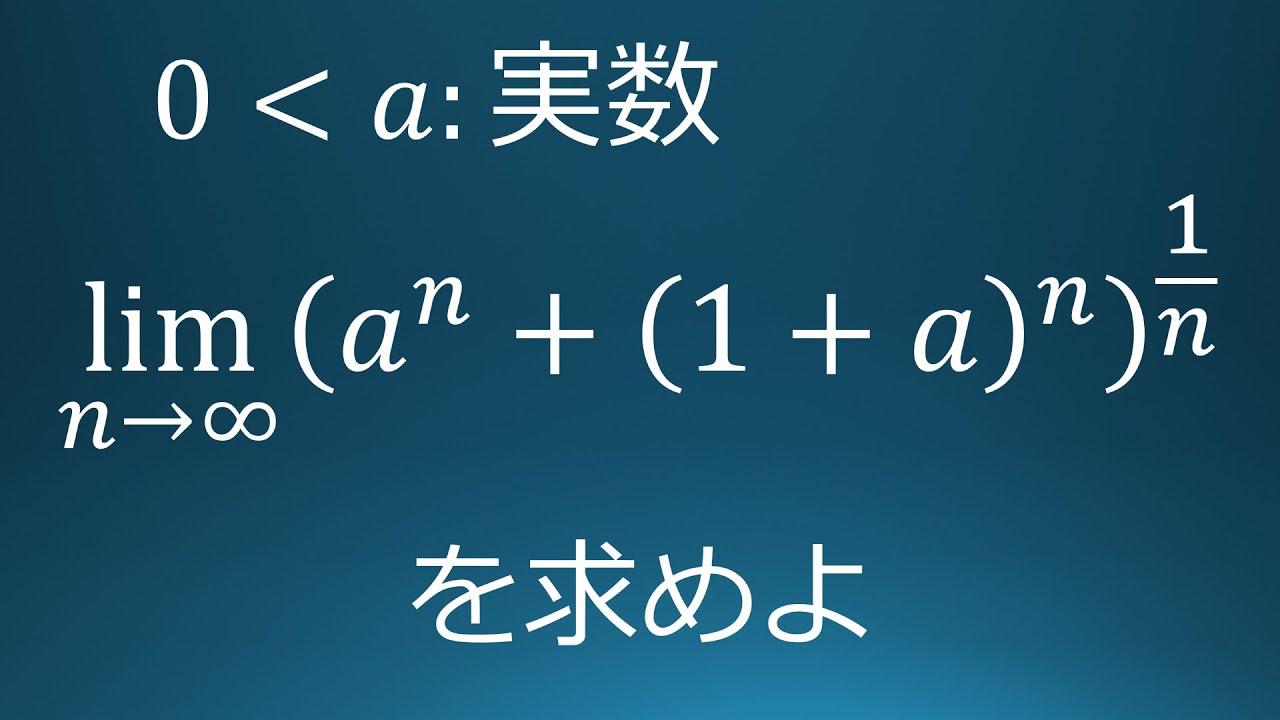問題文全文(内容文):
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$h(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$h(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
単元:
#対数関数#関数と極限
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$h(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$h(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
投稿日:2023.09.01