【数学】中高一貫校問題集2幾何133：円：接弦定理： 相似の証明2 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中３数学 > 円 > 【数学】中高一貫校問題集2幾何133：円：接弦定理： 相似の証明2

【数学】中高一貫校問題集2幾何133：円：接弦定理： 相似の証明2

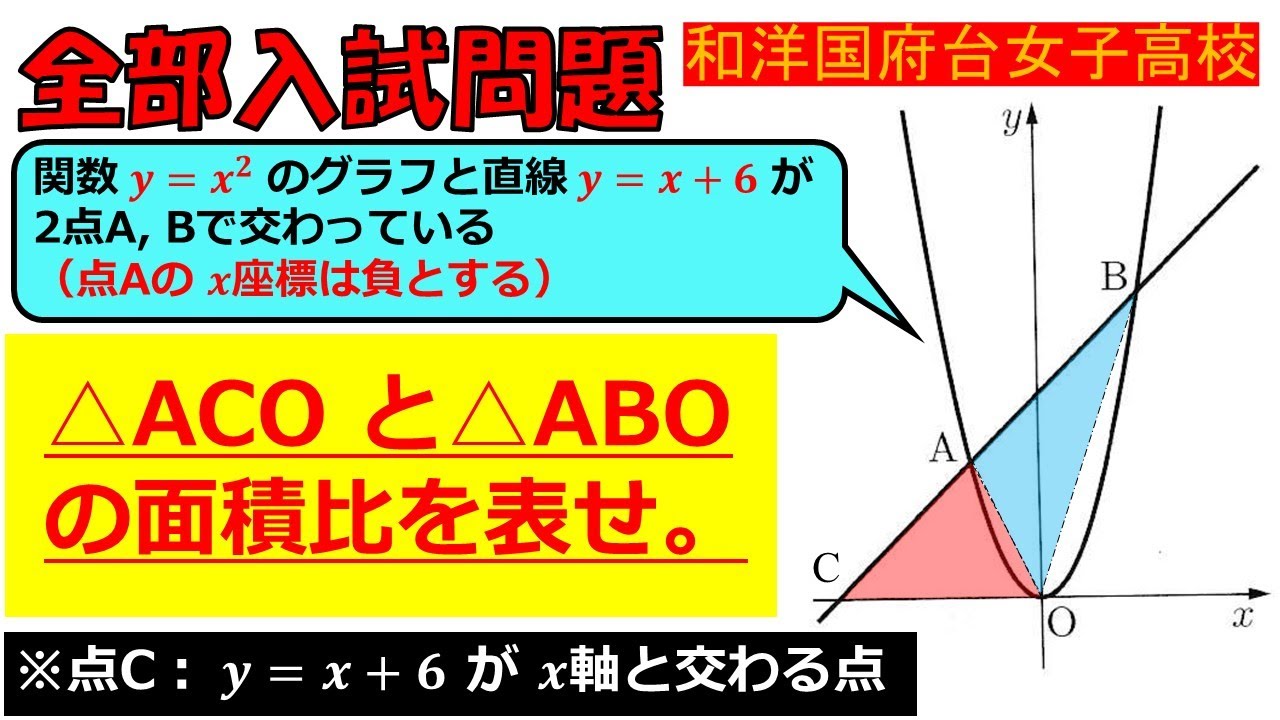
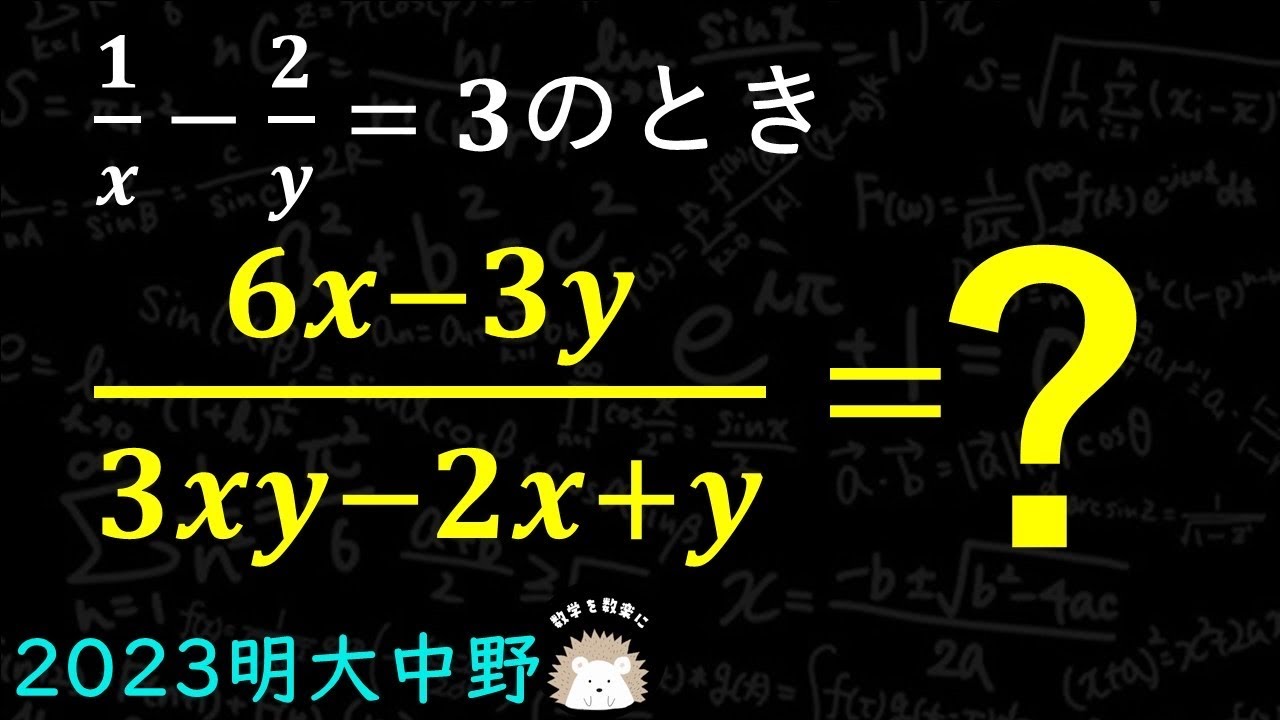問題文全文(内容文)：
右の図のように、円に内接する二等辺三角形ABCがあり、AB=AC=3cm、BC=2cmである。点Bにおける円の接線と辺ACの延長との交点をEとする。また、Cを通り辺ABに平行な直線が円と交わる点をD、BEと交わる点をFとする。
(1)△BCE∽△CFEであることを証明しなさい。
(2)線分CF、EFの長さをそれぞれ求めなさい。
チャプター：

0:00 オープニング
0:05 問題文
0:37 (1)アプローチ
1:33 証明
2:57 (2)解説
5:11 エンディング

単元： #数学(中学生)#中３数学#円
教材： #TK数学#TK数学問題集2(幾何編)#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
右の図のように、円に内接する二等辺三角形ABCがあり、AB=AC=3cm、BC=2cmである。点Bにおける円の接線と辺ACの延長との交点をEとする。また、Cを通り辺ABに平行な直線が円と交わる点をD、BEと交わる点をFとする。
(1)△BCE∽△CFEであることを証明しなさい。
(2)線分CF、EFの長さをそれぞれ求めなさい。
投稿日：2023.11.25

＜関連動画＞

【数学】中高一貫校問題集2幾何120：円：円の接線：内心の性質

アイキャッチ画像
単元： #数学(中学生)#中３数学#円
教材： #TK数学#TK数学問題集2(幾何編)#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
△ABCの内心をIとする。∠A＝64°のとき、∠BICの大きさを求めなさい。
この動画を見る　

【数学】中高一貫校用問題集幾何：三平方の定理：平面図形 折り返した図形2

アイキャッチ画像
単元： #数学(中学生)#中３数学#三平方の定理
教材： #TK数学#TK数学問題集2(幾何編)#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。
この動画を見る　

【中学数学】三平方の定理：正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき(続きは概要欄)

アイキャッチ画像
単元： #数学(中学生)#中３数学#三平方の定理
指導講師： 理数個別チャンネル
問題文全文(内容文)：
正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき、次の問いに答えよう。
(1)線分AHの長さを求めよう。
(2)正四面体OABCの高さOHを求めよう。
(3)正四面体OABCの体積Vを求めよう。
この動画を見る　

文字３つ式２つ

アイキャッチ画像
単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
$
\begin{eqnarray}
\left\{
\begin{array}{l}
5a+2b-c =6 \cdots ① \\
a-3b+2c = 4 \cdots ②
\end{array}
\right.
\end{eqnarray}
$
のとき自然数a,b,c=?

市川高等学校
この動画を見る　

ごめんなさい

アイキャッチ画像
単元： #数学(中学生)#中３数学#平方根#２次方程式#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師： 数学を数楽に
問題文全文(内容文)：
a^2=2＋√3
b^2=2＋√3
b>a>0
abの値を求めよ
a-bの値を求めよ
この動画を見る　
Back to top