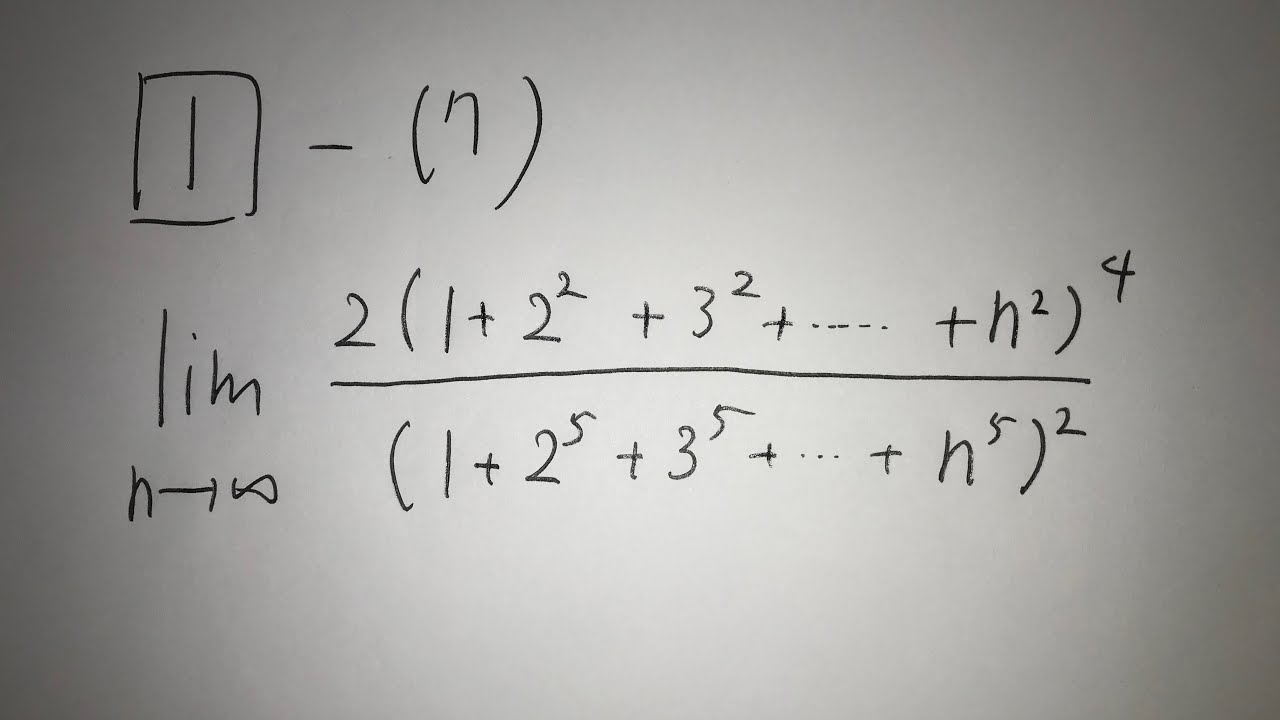これ説明できる？

問題文全文(内容文)：
一筆書きできる確率、一筆書きできない確率

単元： #数列#数学的帰納法#数学(高校生)#数B

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
一筆書きできる確率、一筆書きできない確率

投稿日：2022.04.14

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#明星大学

指導講師：ハクシ高校【数学科】良問演習チャンネル

問題文全文(内容文)：
数列$\{a_n\}$の初項から第$n$項までの和を$S_n$とする。
$S_n=-2a_n+3n$が成り立つとき、次の問いに答えよ。
（1）$a_1$と$a_2$を求めよ。
（2）$a_{n+1}$を$a_n$を用いて表せ。
（3）$a_n$を$n$を用いて表せ。

この動画を見る　

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：【ゼロから理解できる】高校数学・物理

問題文全文(内容文)：
等差数列$-2,1,4,7,10…$について、次の問いに答えよ。
（1）一般項$a_n$を求めよ。
（2）第100項$a_{100}$を求めよ。
（3）初項から第$n$項までの和$S_n$を求めよ。

この動画を見る　

単元： #大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
公差が０でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119　$a_n$を求めよ。

藤田医学科大学

この動画を見る　

単元： #大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#岡山県立大学

指導講師：ますただ

問題文全文(内容文)：
$(1+2+3+・・・+n)^2=1^3+2^3+3^3+・・・+n^3$が成り立つことを示せ。
$n$：自然数

2020年岡山県立大学　入試問題

この動画を見る　

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
$a_1=1,a_2=3$
$a_{n+2}-4a_{n+1}+4a_n=1$
一般項を求めよ.

兵庫県立大過去問

この動画を見る　