 数列
数列
 数列
数列
数列 数B 部分分数分解の応用【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の和Sを求めよ
(1)$S=\dfrac{1}{1・4}+\dfrac{1}{4・7}+\dfrac{1}{7・10}+ ‥ ‥‥+\dfrac{1}{(3n-2)(3n+1)}$
(2)$S=\dfrac{1}{1・3}+\dfrac{1}{2・4}+\dfrac{1}{3・5}+ ‥ ‥‥+\dfrac{1}{n(n+2)}$
和を求めよ
$\displaystyle \sum_{k=1}^n \dfrac{1}{\sqrt{k+2}+\sqrt{k+3} }$
次の数列の初項から第n項までの和を求めよ
(1)$1$,$\dfrac{1}{1+2}$,$\dfrac{1}{1+2+3}$,‥ ‥‥
(2)$\dfrac{3}{1^2}$,$\dfrac{5}{1^2+2^2}$,$\dfrac{7}{1^2+2^2+3^2}$‥ ‥‥
(3)$\dfrac{1}{1×2×3}$,$\dfrac{1}{2×3×4}$,$\dfrac{1}{3×4×5}$‥ ‥‥
この動画を見る
次の和Sを求めよ
(1)$S=\dfrac{1}{1・4}+\dfrac{1}{4・7}+\dfrac{1}{7・10}+ ‥ ‥‥+\dfrac{1}{(3n-2)(3n+1)}$
(2)$S=\dfrac{1}{1・3}+\dfrac{1}{2・4}+\dfrac{1}{3・5}+ ‥ ‥‥+\dfrac{1}{n(n+2)}$
和を求めよ
$\displaystyle \sum_{k=1}^n \dfrac{1}{\sqrt{k+2}+\sqrt{k+3} }$
次の数列の初項から第n項までの和を求めよ
(1)$1$,$\dfrac{1}{1+2}$,$\dfrac{1}{1+2+3}$,‥ ‥‥
(2)$\dfrac{3}{1^2}$,$\dfrac{5}{1^2+2^2}$,$\dfrac{7}{1^2+2^2+3^2}$‥ ‥‥
(3)$\dfrac{1}{1×2×3}$,$\dfrac{1}{2×3×4}$,$\dfrac{1}{3×4×5}$‥ ‥‥
数列 数B Σ公式の応用【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の和を求めよ。
(1)$\displaystyle \sum_{m=1}^n \displaystyle \sum_{k=1}^m (12k-6)$
(2)$\displaystyle \sum_{m=1}^n \displaystyle \sum_{l=1}^m \displaystyle \sum_{k=1}^l k$
次の数列の初項から第n項までの和を求めよ。
(1) $1^2$+$1・2+2^2$、$2^2+2・3+3^2$、$3^3+3・4+4^2$、…
(2) $1^2$、$1^2+3^2$、$1^2+3^2+5^2$、$1^2+3^2+5^2+7^2$、…
次の数列の和を求めよ。
(1) $1・n$, $3・(nー1)$,$5・(nー2)$,・・・・,$(2n -3) • 2$, $(2n-1)•1$
(2) $1^2・n$,$2^2・(nー1)$, $3^2・(nー2)$,・・・,$(n-1)^2・2$,$n^2・1$
次の数列の一般項を求めよ。また、初項から第n項までの和を求めよ。
0,4, 18,48,100,180,294,…
この動画を見る
次の和を求めよ。
(1)$\displaystyle \sum_{m=1}^n \displaystyle \sum_{k=1}^m (12k-6)$
(2)$\displaystyle \sum_{m=1}^n \displaystyle \sum_{l=1}^m \displaystyle \sum_{k=1}^l k$
次の数列の初項から第n項までの和を求めよ。
(1) $1^2$+$1・2+2^2$、$2^2+2・3+3^2$、$3^3+3・4+4^2$、…
(2) $1^2$、$1^2+3^2$、$1^2+3^2+5^2$、$1^2+3^2+5^2+7^2$、…
次の数列の和を求めよ。
(1) $1・n$, $3・(nー1)$,$5・(nー2)$,・・・・,$(2n -3) • 2$, $(2n-1)•1$
(2) $1^2・n$,$2^2・(nー1)$, $3^2・(nー2)$,・・・,$(n-1)^2・2$,$n^2・1$
次の数列の一般項を求めよ。また、初項から第n項までの和を求めよ。
0,4, 18,48,100,180,294,…
数列 数B 約数の和と複利計算【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
初項が1,公比が3である等比数列で、初めて100より大きくなるのは第何項
か。また,初項から第何項までの和が初めて 1000より大きくなるか。
次の数の正の約数の和を求めよ
(1)$3^7$
(2)$3^4×7^3$
(3)864
初項1,公比2,項数nの等比数列において,各項の和、積、逆数の和を,それぞれS,P,Tとするとき,等式$S^n=P^2T^n$が成り立つことを証明せよ。
毎年度初めに1万円ずつ積み立てる。年利率を0.6%とし、1年ごとの複利で第10年度末には元利合計はいくらになるか。ただし,$1.006^10=1.0616$ として計算し,1円未満は切り捨てよ。
この動画を見る
初項が1,公比が3である等比数列で、初めて100より大きくなるのは第何項
か。また,初項から第何項までの和が初めて 1000より大きくなるか。
次の数の正の約数の和を求めよ
(1)$3^7$
(2)$3^4×7^3$
(3)864
初項1,公比2,項数nの等比数列において,各項の和、積、逆数の和を,それぞれS,P,Tとするとき,等式$S^n=P^2T^n$が成り立つことを証明せよ。
毎年度初めに1万円ずつ積み立てる。年利率を0.6%とし、1年ごとの複利で第10年度末には元利合計はいくらになるか。ただし,$1.006^10=1.0616$ として計算し,1円未満は切り捨てよ。
数列 数B 等差数列、等比数列の連立【TAKAHASHI名人がていねいに解説】
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
1問目
初項が1である等比数列a_{n}と、初項2である等比数列b_{n}がある c_{n} = a_{n} + b_{n}とおくとき、c2=6,c3=11,c4=20である 数列c_{n}の一般項を求めよ
2問目
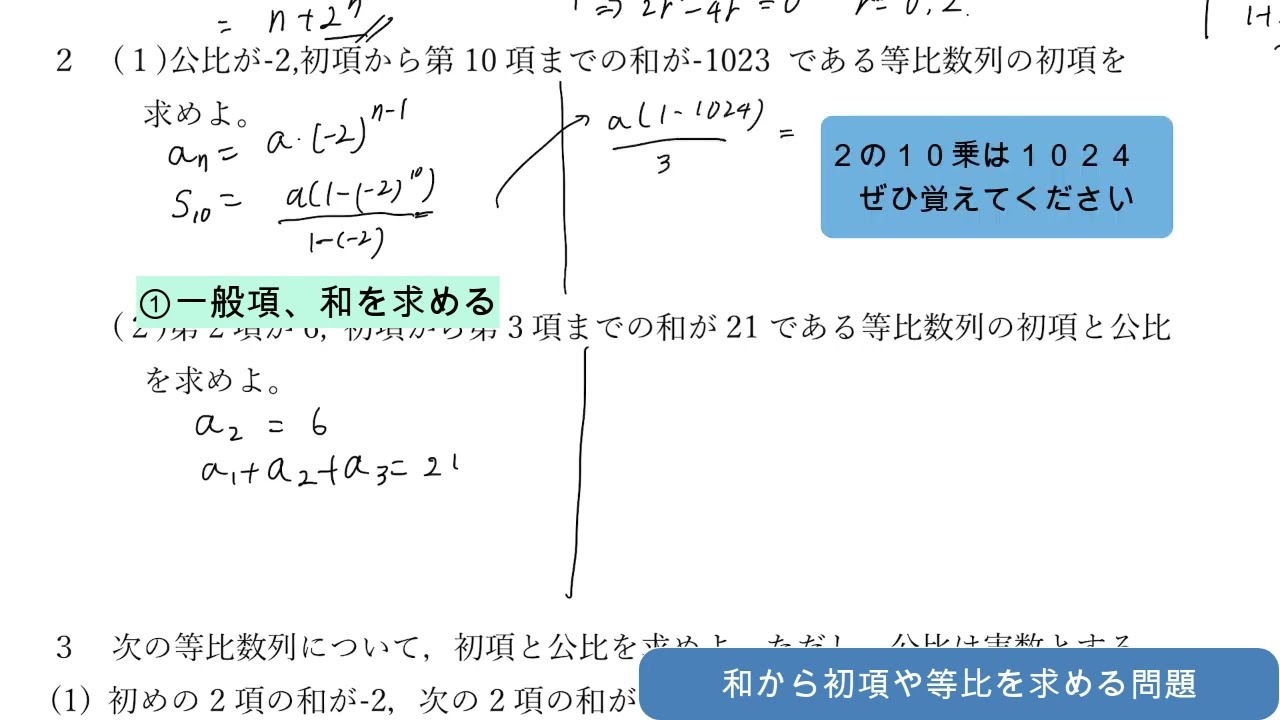
(1)公比-2、初項から第10項までの和が-1023である等比数列の初項を求めよ
(2) 第2項が6、初項から第3項までの和が21である等比数列の初項と公比を求めよ
3問目
次の等比数列について、初項と公比を求めよ。ただし、公比は実数とする。
(1) 初めの2項の和が-2、次の2項の和が-8
(2) 初項から第3項までの和が3、第4項から第6項までの和が-24
4問目
初項から第10項までの和が4、初項から第20項までの和が24である等比数列について、初項から第40項までの和を求めよ。ただし、公比は実数とする
この動画を見る
1問目
初項が1である等比数列a_{n}と、初項2である等比数列b_{n}がある c_{n} = a_{n} + b_{n}とおくとき、c2=6,c3=11,c4=20である 数列c_{n}の一般項を求めよ
2問目
(1)公比-2、初項から第10項までの和が-1023である等比数列の初項を求めよ
(2) 第2項が6、初項から第3項までの和が21である等比数列の初項と公比を求めよ
3問目
次の等比数列について、初項と公比を求めよ。ただし、公比は実数とする。
(1) 初めの2項の和が-2、次の2項の和が-8
(2) 初項から第3項までの和が3、第4項から第6項までの和が-24
4問目
初項から第10項までの和が4、初項から第20項までの和が24である等比数列について、初項から第40項までの和を求めよ。ただし、公比は実数とする
数列 数B 等差数列、等比数列の条件を考える【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
1問目
数列8,a,bが等差数列で、数列a,b,36が等比数列であるとき、a,bの値を求めよ。
2問目
等比数列をなす3つの実数があって,それらの和が19,積が216であるという。これら3つの実数を求めよ。
3問目
数列2, 6,……,954,……がある。この数列は等差数列となることができるか。また等比数列になることができるか。
この動画を見る
1問目
数列8,a,bが等差数列で、数列a,b,36が等比数列であるとき、a,bの値を求めよ。
2問目
等比数列をなす3つの実数があって,それらの和が19,積が216であるという。これら3つの実数を求めよ。
3問目
数列2, 6,……,954,……がある。この数列は等差数列となることができるか。また等比数列になることができるか。
数列 数B 等差数列和の応用【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列$\log_{ 2} a_n$が初項2、公差-1である等差数列であるとき、
数列$a_n$は等比数列であることを示せ。
また、初項と公比を求めよ
この動画を見る
数列$\log_{ 2} a_n$が初項2、公差-1である等差数列であるとき、
数列$a_n$は等比数列であることを示せ。
また、初項と公比を求めよ
福田のおもしろ数学051〜10秒チャレンジ!〜階乗の付いた分数の計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \frac{1}{2!}+\displaystyle \frac{2}{3!}+\displaystyle \frac{3}{4!}+\displaystyle \frac{4}{5!}+\displaystyle \frac{5}{6!}$を計算してください。
この動画を見る
$\displaystyle \frac{1}{2!}+\displaystyle \frac{2}{3!}+\displaystyle \frac{3}{4!}+\displaystyle \frac{4}{5!}+\displaystyle \frac{5}{6!}$を計算してください。
数列 数B 等差数列和の応用【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
1問目
初項が50,公差が -3である等差数列について、次の問いに答えよ。
(1) 第何項が初めて負の数となるか。
(2) 初項から第何項までの和が最大となるか。また,その和を求めよ。
2問目
1から300までの自然数について,次のような数の和を求めよ。
(1) 3または7で割り切れる数
(2) 3でも7でも割り切れない数
3問目
第10項が168,第25 項が408である等差数列について,次の問いに答えよ。
(1) 1000は第何項か。
(2) 初項から第何項までの和が初めて 1000より大きくなるか。
この動画を見る
1問目
初項が50,公差が -3である等差数列について、次の問いに答えよ。
(1) 第何項が初めて負の数となるか。
(2) 初項から第何項までの和が最大となるか。また,その和を求めよ。
2問目
1から300までの自然数について,次のような数の和を求めよ。
(1) 3または7で割り切れる数
(2) 3でも7でも割り切れない数
3問目
第10項が168,第25 項が408である等差数列について,次の問いに答えよ。
(1) 1000は第何項か。
(2) 初項から第何項までの和が初めて 1000より大きくなるか。
福田のおもしろ数学020〜わんちゃんの男の子と女の子の比率は〜Google入社試験の類題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか
この動画を見る
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか
福田の数学〜0と1の間に整数は存在しないなんて当たり前〜東京大学2018年文系第2問〜数列の増減と整数となる条件

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数列$a_{ 1},a_{ 2 }$,・・・を$a_{ n }=\displaystyle \frac{{}_2n \mathrm{ C }_n}{n!}$(n=1,2,・・・)で定める。
(1)$a_{ 7 }$と1の大小を調べよ。
(2)$n \geqq 2$とする。$\displaystyle \frac{a_{ n }}{a_{ n-1}}<1を満たすnの範囲を求めよ。$
(3)$a_{ n }$が整数となる$n \geqq 1$を全て求めよ。
この動画を見る
数列$a_{ 1},a_{ 2 }$,・・・を$a_{ n }=\displaystyle \frac{{}_2n \mathrm{ C }_n}{n!}$(n=1,2,・・・)で定める。
(1)$a_{ 7 }$と1の大小を調べよ。
(2)$n \geqq 2$とする。$\displaystyle \frac{a_{ n }}{a_{ n-1}}<1を満たすnの範囲を求めよ。$
(3)$a_{ n }$が整数となる$n \geqq 1$を全て求めよ。
福田の数学〜ポリアの壺とは逆の試行における確率の極限〜杏林大学2023年医学部第1問後編〜確率漸化式と極限

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
この動画を見る
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
福田の数学〜ポリアの壺は証明を覚えよう〜杏林大学2023年医学部第1問前編〜ポリアの壺

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
この動画を見る
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
福田の数学〜回転の概念を使って考えるよ〜北里大学2023年医学部第3問〜ベクトルの漸化式と点列
単元:
#大学入試過去問(数学)#平面上のベクトル#数列#ベクトルと平面図形、ベクトル方程式#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
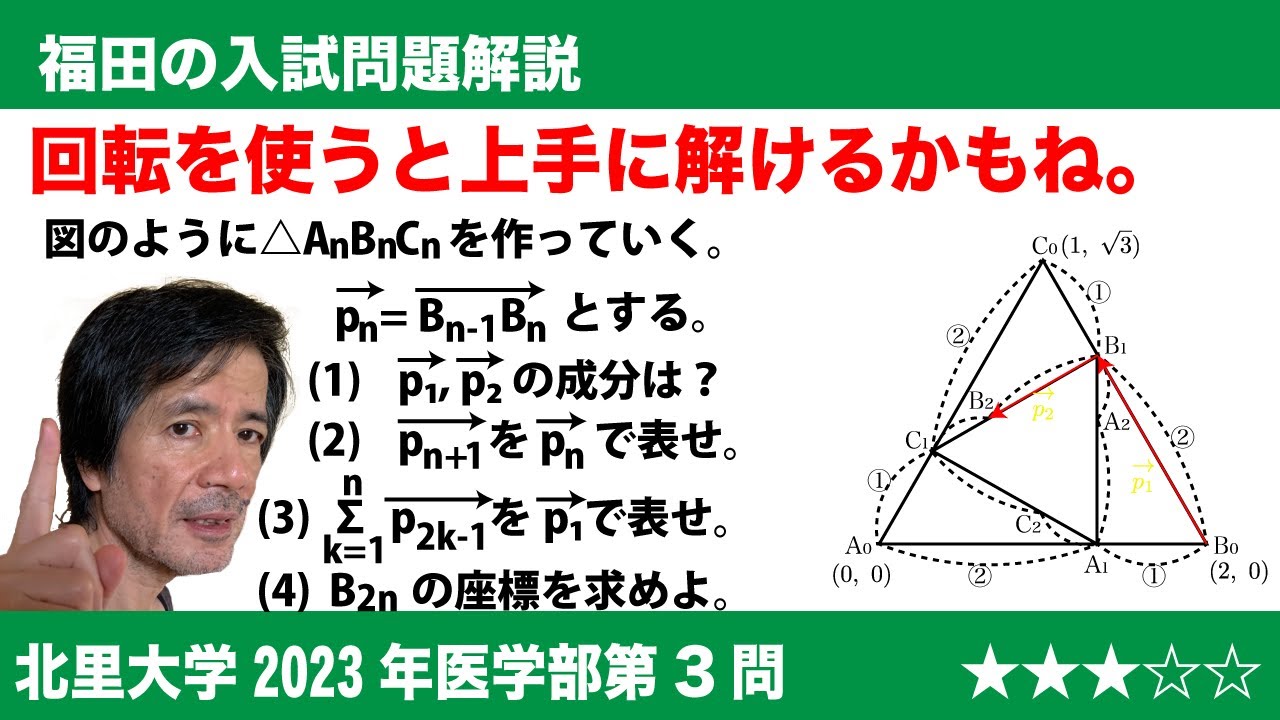
座標平面上に 3 点 $A_{0} ( 0 , 0 ), B_{0} ( 2 , 0 ), C_{0}( 1 ,\sqrt{ 3 })$があり、線分$A_{0}B_{0},B_{0}C_{0},C_{0}A_{0}$をそれぞれ 2 : 1 に内分する点 $A_{1} ,B_{1} ,C_{1}$をとる。以下同様にして、正の整数nに対し、線分$A_{n}B_{n},B_{n}C_{n},C_{n}A_{n}$をそれぞれ 2 : 1 に内分する点$A_{n+1},B_{n+1},C_{n+1}$をとる。また、$\overrightarrow{ P_{n} }=\overrightarrow{ B_{n-1}B_{n} }(n=1,2,3,・・・)$とおく。
(1)$\overrightarrow{ p_{1} },\overrightarrow{ p_{2} }$をそれぞれ成分表示せよ。
(2)$\overrightarrow{ p_{n+2} }を\overrightarrow{ p_{n} }$を用いて表せ。
(3)$\displaystyle \sum_{k=1}^n \overrightarrow{ p_{2k-1}}$を$\overrightarrow{ p-1}$を用いて表せ。
(4)点B_{2n}の座標を求めよ。
この動画を見る
座標平面上に 3 点 $A_{0} ( 0 , 0 ), B_{0} ( 2 , 0 ), C_{0}( 1 ,\sqrt{ 3 })$があり、線分$A_{0}B_{0},B_{0}C_{0},C_{0}A_{0}$をそれぞれ 2 : 1 に内分する点 $A_{1} ,B_{1} ,C_{1}$をとる。以下同様にして、正の整数nに対し、線分$A_{n}B_{n},B_{n}C_{n},C_{n}A_{n}$をそれぞれ 2 : 1 に内分する点$A_{n+1},B_{n+1},C_{n+1}$をとる。また、$\overrightarrow{ P_{n} }=\overrightarrow{ B_{n-1}B_{n} }(n=1,2,3,・・・)$とおく。
(1)$\overrightarrow{ p_{1} },\overrightarrow{ p_{2} }$をそれぞれ成分表示せよ。
(2)$\overrightarrow{ p_{n+2} }を\overrightarrow{ p_{n} }$を用いて表せ。
(3)$\displaystyle \sum_{k=1}^n \overrightarrow{ p_{2k-1}}$を$\overrightarrow{ p-1}$を用いて表せ。
(4)点B_{2n}の座標を求めよ。
福田の数学〜整数部分の評価が難しい問題〜北里大学2023年医学部第1問(3)〜漸化式と整数部分の評価

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a=3+\sqrt{10},b=3-\sqrt{10}とし、正の整数nに対してA_{n}=a^n+b^nとおく。
このとき、A_{2} ,A_{3}の値はそれぞれA_{2}=\fbox{ク},A_{3}=\fbox{ケ}であり、A_{n+2}をA_{n+1},A_{n}を用いて表すとA_{n+2}=\fbox{コ}である。
また、a^111の整数部分をkとするとき、kを10で割ると$ \fbox{サ}$余る。
この動画を見る
$a=3+\sqrt{10},b=3-\sqrt{10}とし、正の整数nに対してA_{n}=a^n+b^nとおく。
このとき、A_{2} ,A_{3}の値はそれぞれA_{2}=\fbox{ク},A_{3}=\fbox{ケ}であり、A_{n+2}をA_{n+1},A_{n}を用いて表すとA_{n+2}=\fbox{コ}である。
また、a^111の整数部分をkとするとき、kを10で割ると$ \fbox{サ}$余る。
例のアレ

単元:
#数列とその和(等差・等比・階差・Σ)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{1}{1×2×3×4}+\displaystyle \frac{1}{2×3×4×5}+\displaystyle \frac{1}{3×4×5×6}$$+…+\displaystyle \frac{1}{6×7×8×9}+\displaystyle \frac{1}{7×8×9×10}$
この動画を見る
$\displaystyle \frac{1}{1×2×3×4}+\displaystyle \frac{1}{2×3×4×5}+\displaystyle \frac{1}{3×4×5×6}$$+…+\displaystyle \frac{1}{6×7×8×9}+\displaystyle \frac{1}{7×8×9×10}$
【保存版】計算の裏技

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1~50までの足し算を一気にする裏技に関して解説していきます。
この動画を見る
1~50までの足し算を一気にする裏技に関して解説していきます。
さくらんぼだけでスイカを作ると何円?

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
スイカゲームでさくらんぼだけでスイカを作るのにおかかる値段を計算していきます。
この動画を見る
スイカゲームでさくらんぼだけでスイカを作るのにおかかる値段を計算していきます。
福田の数学〜部分和と漸化式の扱い方〜慶應義塾大学2023年経済学部第2問〜部分和と漸化式

単元:
#大学入試過去問(数学)#数列#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_{n}\}$に対して$\displaystyle \sum_{k=1}^n a_k(n=1,2,3,・・・)$とし、さらに$S_0=0$と定める。$\{a_n\}$は$S_n=\dfrac{1}{4}-\dfrac{1}{2}(n+3)a_{n+1}$(n=0,1,2,・・・)を満たすとする。
(1)$a_1=\dfrac{\fbox{ア}}{\fbox{イ}}$である。また、$n \geqq 1$に対して$a_n=S_n-S_{n-1}$であるから、関係式$(n+\fbox{ウ})a_{n+1}=(n+\fbox{エ})a_n (n=1,2,3,・・・)$・・・(*)が得られる。数列$\{{b_n}\}$を$b_n=n(n+1)(n+2)a_n (n=1,2,3,・・・)$で定めると、$b_1=\fbox{オ}$であり、$n \geqq 1$に対して$b_{n+1}=\fbox{カ}b_n$が成り立つ。ゆえに$a_n=\dfrac{\fbox{キ}}{n(n+1)(n+2)}$が得られる。
次に、数列$\{{T_n}\}=\displaystyle \sum_{k=1}^n \dfrac{a_k}{(k+3)(k+4)}(n=1,2,3,・・・)$で定める。
(2)(*)より導かれる関係式
$\dfrac{a_k}{k+3}-\dfrac{a_{k+1}}{k+4}=\dfrac{\fbox{ク}a_k}{(k+3)(k+4)} (k=1,2,3,・・・)$
を用いると
$T_n=A-\dfrac{\fbox{ケ}}{\fbox{コ}(n+p)(n+q)(n+r)(n+s)}(n=1,2,3,・・・)$
が得られる。ただしここに$A=\fbox{サ}{シス}$であり、$p \lt q\lt r \lt s$として$p=\fbox{セ},q=\fbox{ソ},r=\fbox{タ},s=\fbox{チ}$である。
(3)不等式$|T_n-A| \lt\dfrac{1}{10000(n+1)(n+2)}$を満たす最小の自然数$nはn=\fbox{ツテ}$である。
この動画を見る
数列$\{a_{n}\}$に対して$\displaystyle \sum_{k=1}^n a_k(n=1,2,3,・・・)$とし、さらに$S_0=0$と定める。$\{a_n\}$は$S_n=\dfrac{1}{4}-\dfrac{1}{2}(n+3)a_{n+1}$(n=0,1,2,・・・)を満たすとする。
(1)$a_1=\dfrac{\fbox{ア}}{\fbox{イ}}$である。また、$n \geqq 1$に対して$a_n=S_n-S_{n-1}$であるから、関係式$(n+\fbox{ウ})a_{n+1}=(n+\fbox{エ})a_n (n=1,2,3,・・・)$・・・(*)が得られる。数列$\{{b_n}\}$を$b_n=n(n+1)(n+2)a_n (n=1,2,3,・・・)$で定めると、$b_1=\fbox{オ}$であり、$n \geqq 1$に対して$b_{n+1}=\fbox{カ}b_n$が成り立つ。ゆえに$a_n=\dfrac{\fbox{キ}}{n(n+1)(n+2)}$が得られる。
次に、数列$\{{T_n}\}=\displaystyle \sum_{k=1}^n \dfrac{a_k}{(k+3)(k+4)}(n=1,2,3,・・・)$で定める。
(2)(*)より導かれる関係式
$\dfrac{a_k}{k+3}-\dfrac{a_{k+1}}{k+4}=\dfrac{\fbox{ク}a_k}{(k+3)(k+4)} (k=1,2,3,・・・)$
を用いると
$T_n=A-\dfrac{\fbox{ケ}}{\fbox{コ}(n+p)(n+q)(n+r)(n+s)}(n=1,2,3,・・・)$
が得られる。ただしここに$A=\fbox{サ}{シス}$であり、$p \lt q\lt r \lt s$として$p=\fbox{セ},q=\fbox{ソ},r=\fbox{タ},s=\fbox{チ}$である。
(3)不等式$|T_n-A| \lt\dfrac{1}{10000(n+1)(n+2)}$を満たす最小の自然数$nはn=\fbox{ツテ}$である。
【FULL】定期テスト直前対策!数列解説動画フルパック流し【数B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列のまとめ動画です。
等差数列・等比数列の基本から数学的帰納法・確率漸化式まで
見たい内容のシーンをチャプターから選んで下さい!!
この動画を見る
数列のまとめ動画です。
等差数列・等比数列の基本から数学的帰納法・確率漸化式まで
見たい内容のシーンをチャプターから選んで下さい!!
高知大 漸化式の基本問題

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
各項は正である数列$a_n$の和を$S_n$とする
$S_n=\frac{1}{2}{a_n}^2+\frac{1}{2}{a_n}-1$
が成り立つとき、一般項$a_n$を求めよ
高知大学2012年過去問
この動画を見る
各項は正である数列$a_n$の和を$S_n$とする
$S_n=\frac{1}{2}{a_n}^2+\frac{1}{2}{a_n}-1$
が成り立つとき、一般項$a_n$を求めよ
高知大学2012年過去問
信州大 連立漸化式
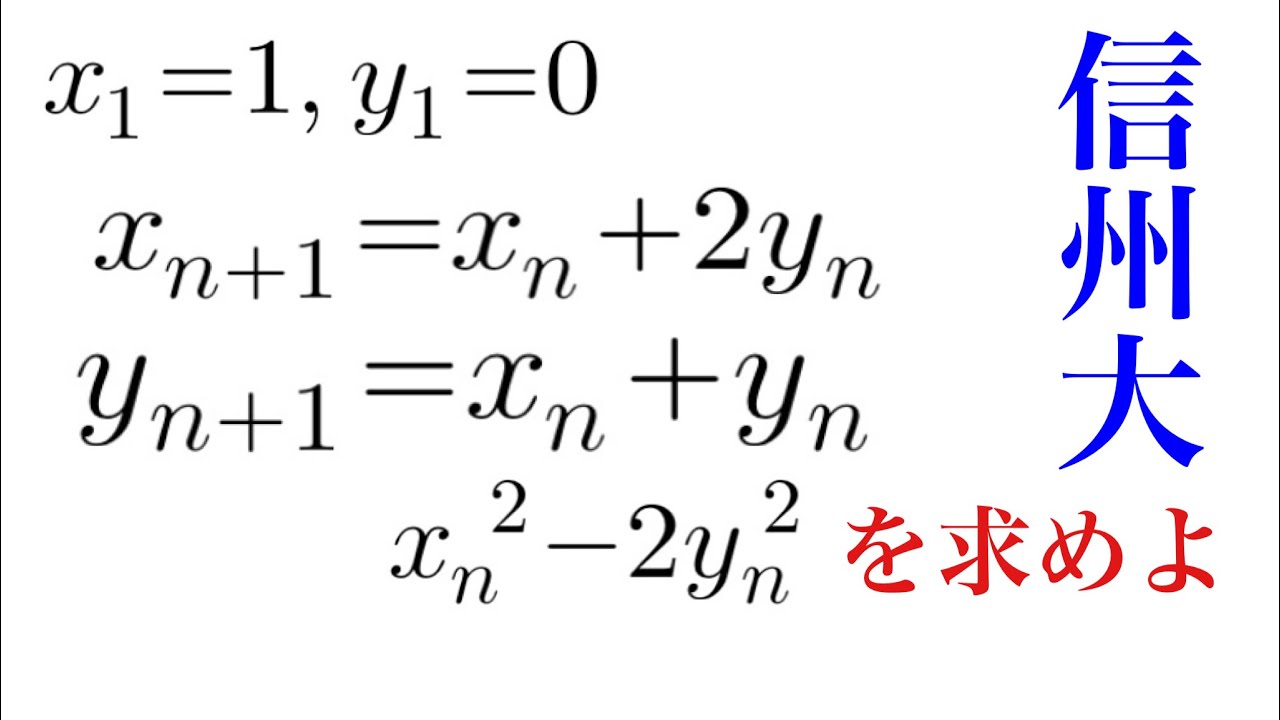
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x_1=1,y_1=0$
$x_{n+1}=x_n+2y_n$
$y_{n+1}=x_n+y_n$
このとき、${x_n}^2-2{y_n}^2$を求めよ
この動画を見る
$x_1=1,y_1=0$
$x_{n+1}=x_n+2y_n$
$y_{n+1}=x_n+y_n$
このとき、${x_n}^2-2{y_n}^2$を求めよ
熊本大(理)漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
一般項を求めよ
$a_1=\displaystyle \frac{1}{8}$
$(4n^2-1)(a_n-a_{n+1})=8(n^2-1)a_na_{n+1}$
熊本大学理学部過去問
この動画を見る
一般項を求めよ
$a_1=\displaystyle \frac{1}{8}$
$(4n^2-1)(a_n-a_{n+1})=8(n^2-1)a_na_{n+1}$
熊本大学理学部過去問
熊本大(文)漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
一般項を求めよ
$a_1=\displaystyle \frac{2}{3}$
$2(a_n-a_{n+1})=(n+2)a_na_{n+1}$
熊本大学文学部
この動画を見る
一般項を求めよ
$a_1=\displaystyle \frac{2}{3}$
$2(a_n-a_{n+1})=(n+2)a_na_{n+1}$
熊本大学文学部
数列 数B 等差数列基本1【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
1問目
nは自然数の定数とする。次の数列の第k項をkの式で表せ
2問目
(1)等差数列 100,94,88,……において,第何項が初めて負の数となるか。
(2)等差数列5,9, 13,………において,第何項が初めて100より大きくなるか。
3問目
一般項が an =3―4nで表される数列(an) がある。数列(an)の項を,初項から2つおきにとってできる数列 a1,a2,a3…….は等差数列であることを示せ。また,初項と公差を求めよ。
4問目
数列 (an),(bn)が等差数列ならば,次の数列も等差数列であることを証明せよ。
(1) a5n
(2) {2an -3bn}
(3) {a2n + b3n}
この動画を見る
1問目
nは自然数の定数とする。次の数列の第k項をkの式で表せ
2問目
(1)等差数列 100,94,88,……において,第何項が初めて負の数となるか。
(2)等差数列5,9, 13,………において,第何項が初めて100より大きくなるか。
3問目
一般項が an =3―4nで表される数列(an) がある。数列(an)の項を,初項から2つおきにとってできる数列 a1,a2,a3…….は等差数列であることを示せ。また,初項と公差を求めよ。
4問目
数列 (an),(bn)が等差数列ならば,次の数列も等差数列であることを証明せよ。
(1) a5n
(2) {2an -3bn}
(3) {a2n + b3n}
数列 数B 等差数列基本【TAKAHASHI名人がていねいに解説】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
1問目
次のような3つの数、5つの数を求めよ。
(1) 3つの数は等差数列をなし、和は15,2乗の和は83
(2) 3つの数は等差数列をなし、和は21,積は-224
(3) 5つの数は等差数列をなし,和は5,2乗の和は45
2問目
次の数列は、各項の逆数をとったものを順に並べてできる数列が等差数列となる。このとき,x, yの値ともとの数列の一般項を求めよ。
3問目
ある等差数列の初項から第n頭までの和をSnとすると、S10=100, S20=400である。この数列の初項から第30項までの和を求めよ。
この動画を見る
1問目
次のような3つの数、5つの数を求めよ。
(1) 3つの数は等差数列をなし、和は15,2乗の和は83
(2) 3つの数は等差数列をなし、和は21,積は-224
(3) 5つの数は等差数列をなし,和は5,2乗の和は45
2問目
次の数列は、各項の逆数をとったものを順に並べてできる数列が等差数列となる。このとき,x, yの値ともとの数列の一般項を求めよ。
3問目
ある等差数列の初項から第n頭までの和をSnとすると、S10=100, S20=400である。この数列の初項から第30項までの和を求めよ。
そりゃー漸化式でも出せるよね

単元:
#数列
指導講師:
鈴木貫太郎
問題文全文(内容文):
n人を3つのグループに分ける場合の数を$a_{n}$通りとする
$a_{n+1}$と$a_{n}$の関係を式で表せ
$a_{n}$を求めよ$(n \geqq 3)$
この動画を見る
n人を3つのグループに分ける場合の数を$a_{n}$通りとする
$a_{n+1}$と$a_{n}$の関係を式で表せ
$a_{n}$を求めよ$(n \geqq 3)$
茨城大 漸化式ぐらい自由に解かせてくれ

単元:
#数列#学校別大学入試過去問解説(数学)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023茨城大学過去問題
一般項$a_{n}$を求めよ
$3a_{n}=S_{n}+n^2-2n+1$
$S_n=\displaystyle\sum_{k=1}^{n}a_{k}$
この動画を見る
2023茨城大学過去問題
一般項$a_{n}$を求めよ
$3a_{n}=S_{n}+n^2-2n+1$
$S_n=\displaystyle\sum_{k=1}^{n}a_{k}$
【数B】数列:漸化式と数学的帰納法:三項間漸化式 PRIME B 85(1)

単元:
#数列#漸化式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のように定められた数列{aₙ}の一般項を求めよ。
$a_1=1$,$a_2=2$,$a_{n+2}=4a_{n+1}-3a_{n}
この動画を見る
次のように定められた数列{aₙ}の一般項を求めよ。
$a_1=1$,$a_2=2$,$a_{n+2}=4a_{n+1}-3a_{n}
【数B】数列:漸化式と数学的帰納法:分数型の漸化式 PRIME B 81

単元:
#数列#漸化式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のように定められた数列{aₙ}の一般項を求めよ。
$a_1=1$,$a_{n+1}=\displaystyle \frac{a_n}{2a_n+5}$
この動画を見る
次のように定められた数列{aₙ}の一般項を求めよ。
$a_1=1$,$a_{n+1}=\displaystyle \frac{a_n}{2a_n+5}$
ちょっと変わった漸化式 和歌山大

単元:
#数列#漸化式#和歌山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022和歌山大学過去問題
$a_{1}=\frac{1}{2}$,$a_{n+1}=\frac{2}{1+a_{n}}$
$b_{1}=1$,$a_{n}b_{n+1}=b_{n}$
数列$b_{n}$の三項間漸化式をつくれ
$a_{n}$の一般項を求めよ
この動画を見る
2022和歌山大学過去問題
$a_{1}=\frac{1}{2}$,$a_{n+1}=\frac{2}{1+a_{n}}$
$b_{1}=1$,$a_{n}b_{n+1}=b_{n}$
数列$b_{n}$の三項間漸化式をつくれ
$a_{n}$の一般項を求めよ
